A narrow monochromatic beam of light of intensity 1 is incident on a glass plate as shown in figure Another identical glass plate is kept close to the first one and parallel to it. Each glass plate reflects `25%` of the light incident on it and transmits intensities in the interference pattern formed by two beams obtained after one reflection at each plate.
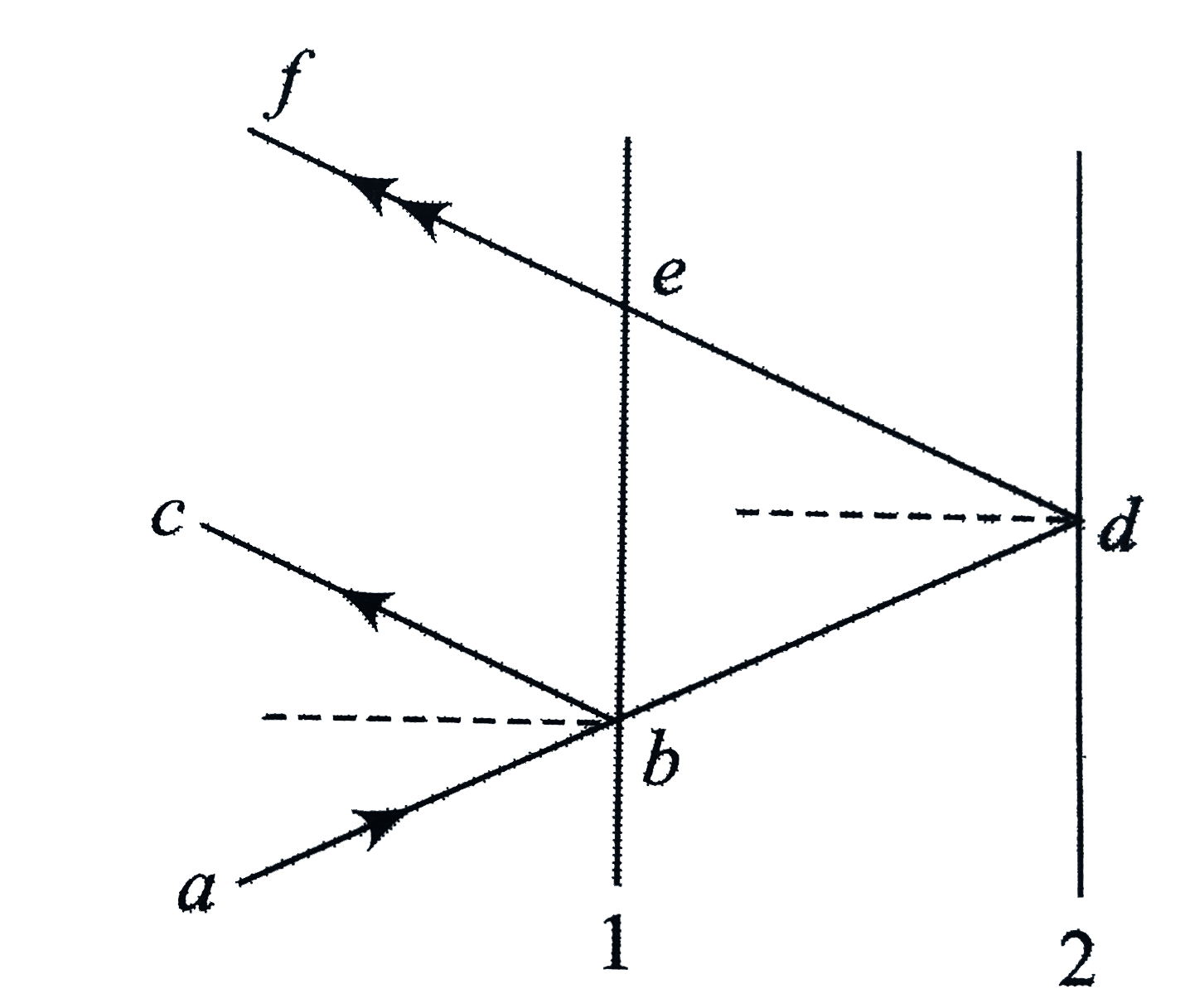
A narrow monochromatic beam of light of intensity 1 is incident on a glass plate as shown in figure Another identical glass plate is kept close to the first one and parallel to it. Each glass plate reflects `25%` of the light incident on it and transmits intensities in the interference pattern formed by two beams obtained after one reflection at each plate.


Text Solution
Verified by Experts
Let `I` be the intensity of beam no. `1` incident on first glass plate. Fig. It is partially reflected and partially transmitted. As each plate reflects `25%` of light falling on it and transmits `75%`. therefore, as is clear from Fig.
`I_(2) = (25)/(100)I = (I)/(4)` `I_(3) = (75)/(100)I = (3)/(4)I`
`I_(4) = (25)/(100)I_(3) = (1)/(4) xx (3)/(4) = (3)/(16)I` `I_(5) = (75)/(100)I_(4) = (3)/(4) xx (3)/(16)I = (9)/(64)I`
If `a` and `b` are amplitude of beam `I_(2)` and `I_(5)`.
when `I_(2) = (I)/(4) = Ka^(2)` or `a = sqrt((I)/(4 K)) = (1)/(2) sqrt((I)/(K))`
`I_(5) = (9)/(64)I = Kb^(2)` or `b = sqrt((9 I)/(64 K)) = (3)/(8) sqrt((1)/(K))`
`(I_(min))/(I_(max)) = ((a - b)^(2))/(a + b)^(2) = (((1)/(2) - (3)/(8))^(2) I//K)/(((1)/(2) + (3)/(8))^(2) I//K) = ((1)/(8))^(2)/((7)/(8))^(2) = (1)/(49)`
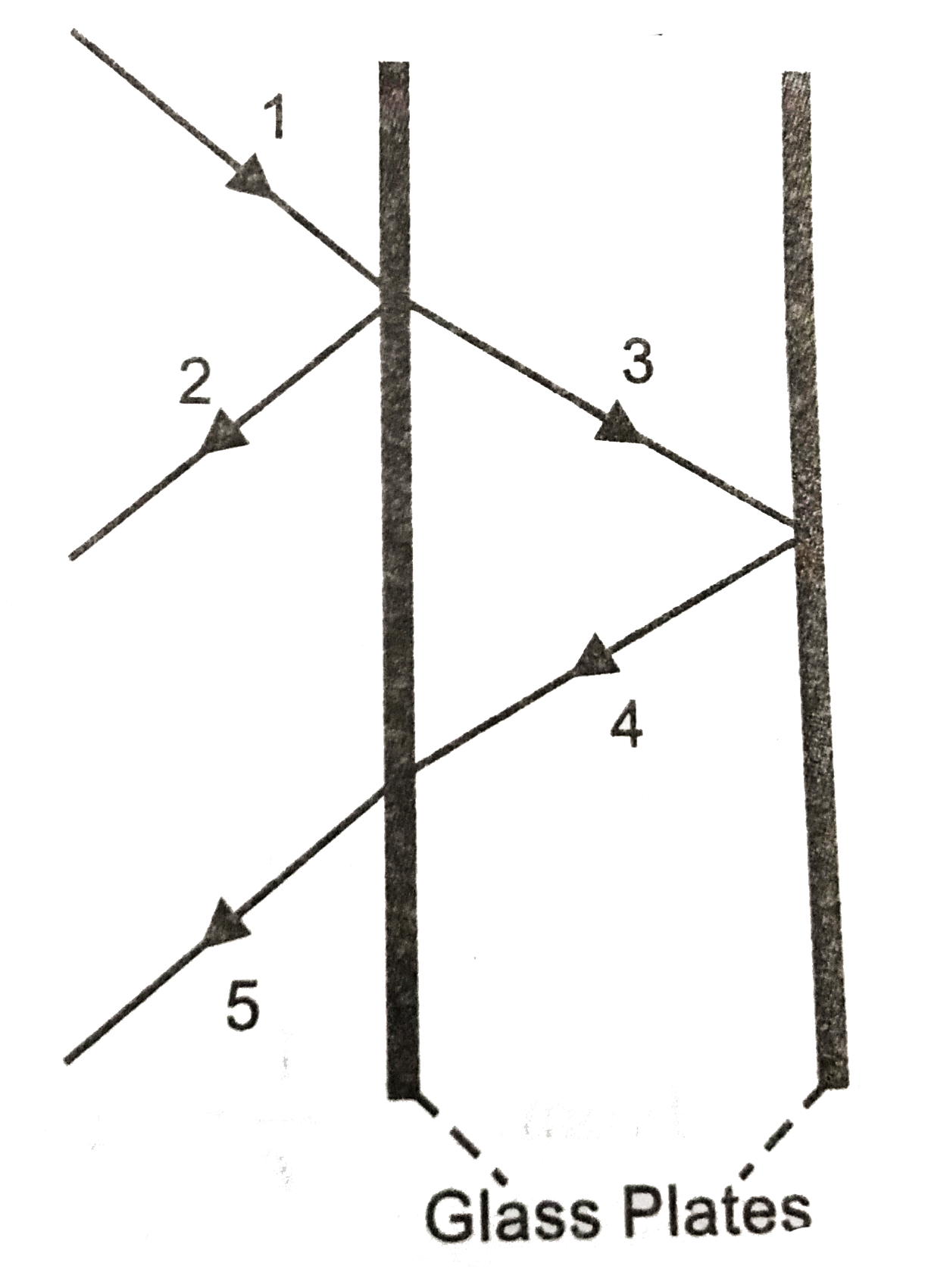
`I_(2) = (25)/(100)I = (I)/(4)` `I_(3) = (75)/(100)I = (3)/(4)I`
`I_(4) = (25)/(100)I_(3) = (1)/(4) xx (3)/(4) = (3)/(16)I` `I_(5) = (75)/(100)I_(4) = (3)/(4) xx (3)/(16)I = (9)/(64)I`
If `a` and `b` are amplitude of beam `I_(2)` and `I_(5)`.
when `I_(2) = (I)/(4) = Ka^(2)` or `a = sqrt((I)/(4 K)) = (1)/(2) sqrt((I)/(K))`
`I_(5) = (9)/(64)I = Kb^(2)` or `b = sqrt((9 I)/(64 K)) = (3)/(8) sqrt((1)/(K))`
`(I_(min))/(I_(max)) = ((a - b)^(2))/(a + b)^(2) = (((1)/(2) - (3)/(8))^(2) I//K)/(((1)/(2) + (3)/(8))^(2) I//K) = ((1)/(8))^(2)/((7)/(8))^(2) = (1)/(49)`

Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
A narrow monochromatic beam of light of intensity I is incident on a galss plate as shown in figure. Another identical glass plate is kept close to the first one & parallel to it. Each glass plate reflects 25% of the light incident on it % transmits the remaining find the ratio of the minimum & the maximum intensities in the interference pattern formed by the two beams obtained after one reflection at each plate.
A narrow monochromatic beam of light of intensity I is incident on a glass plate. Another identical glass plate is kept close to the first one and parallel to it. Each plate reflects 25% of the incident light and transmits the remaining. Calculate the ratio of minimum and maximum intensity in the interference pattern fromed by two beams obtained after reflection from each plate.
A ray light of intensity I is incident on a parallel glass-slab at a point A as shown in figure it undergoes partial reflection and refraction. At each reflection 20% of incident energy is refracted rays AB and A'B' undergo interference find the ratio I_(max)//I_(min)
A ray of light intensity I is incident on a parallel glass-slab at a point A as shown in figure. It undergoes partial reflection and refraction. At each reflection 25% of incident energy is reflected. The rays AB and A^(')B^(') undergo interference. The ratio I_(max)//I_(min) is
Two thin glass plates are placed parallel to each other such that distance between them is very small. Each glass plate reflects 25% of incident energy and transmits remaining 75% Light beam is incident on this system. Consider the interference of two light beams obtained after one reflection from each glass plate. Calculate ratio of the maximum to minimum intensity.
A parallel beam of light of intensity I is incident on a glass plate. 25% of light is reflected in any reflection by upper surface and 50% of light is reflected by any reflection from lower surface. Rest is refracted The ratio of maximum to minimum intensity in interference region of reflected rays is
A ray of light of intensity I is incident on a parallel glass slab at a point A as show. It undergoes partial reflection and refraction. At each reflaction 25% of incident energy is reflected. The rays AB and A'B' undergo interference. The ratio I_(max)//I_(min) is
A ray of unpolarised light is incident on a glass plate of refractive index 1.54 at polarising angle, then angle of refraction is :
A ray of light in incident on a glass plate at an angle of 60^@ . What is the refractive index of glass if the reflected and refracted rays are perpendicular to each other?