A projectile of mass m, charge Z', initial speed v and impact parameter b is scattered by a heavy nucleus of charge Z. Use angular momentum and energy conservation to obtain a formula connecting the minimum distance (s) of the projectile form the nucleus to these parameters .show that for b=0, s reduces to the closest distance of approach `r_0`.
A projectile of mass m, charge Z', initial speed v and impact parameter b is scattered by a heavy nucleus of charge Z. Use angular momentum and energy conservation to obtain a formula connecting the minimum distance (s) of the projectile form the nucleus to these parameters .show that for b=0, s reduces to the closest distance of approach `r_0`.
Text Solution
Verified by Experts
Charge on the nucleus =Ze
Charge on the projectile =Z'e
At infinity, angular momentum of projectile about the nucleus=mvb.
At the point of minimum distance (s) form the nucleus, velocity v' of the projectile is normal to the radius vector (form the centre of nucleus to projectile) , fig.
`:. ` Angular momentum to projectile about the nucleus =mv's
According to the law of conservation of angular momentum
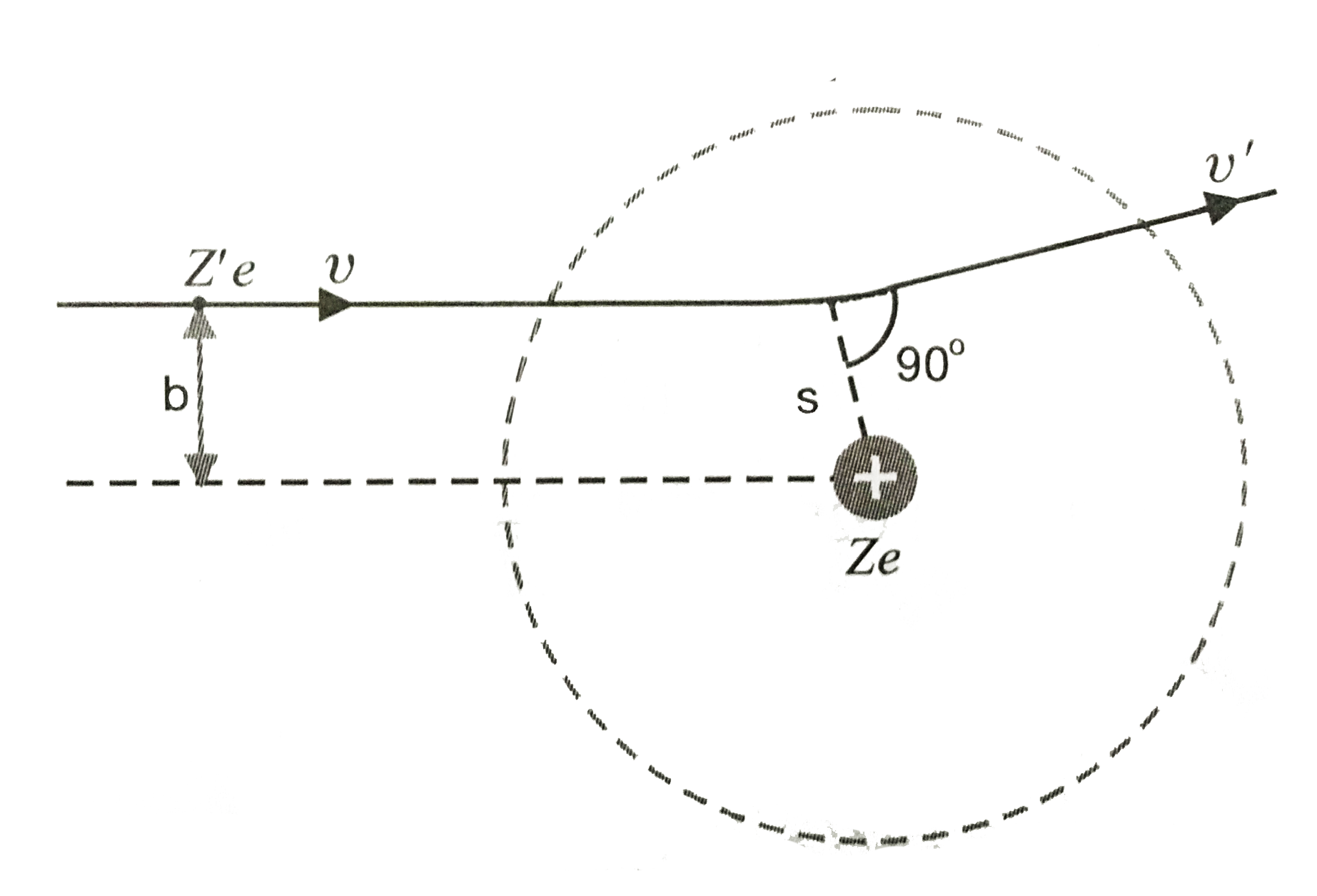
`mv's=mvb or v'=(vb)/s....(i)`
Now, at infinity, K.E. of particle =`1/2 mv^2`
and P.E.=0
At the minimum distance s, K.E of particle =`1/2mv'^2`
P.E of particle `=1/(4pi in_0) ((Ze)(Z'e))/s`
According to the principle of energy conservation,
`1/2mv'^2+1/(4pi in_0) (Z Z'e^2)/s=1/2 mv^2`
Using (1) we get,
`1/2mv^2 (b^2)/(s^2)+1/(4pi in_0) (Z Z'e^2)/s=1/2mv^2`
or `1/2mv^(2)b^(2)+1/(4pi in_0) Z Z'e^2.s=1/2mv^2s^2`
Dividing both sides by `(1/2mv^2)`, we get,
`b^2+1/(2pi in_0) (Z Z'e^2 s)/(mv^2)=s^2`
for a head on collision, b=0
`:. s^2=1/(2pi in_0) (Z Z'e^2 s)/(mv^2)`
or `s=1/(2pi in_0) (Z Z'e^2)/(mv^2)=1/(4pi in_0) ((Ze)(Z'e))/((1/2 mv^2))`
Which is `r_0`, the distance of closest approach.
Charge on the projectile =Z'e
At infinity, angular momentum of projectile about the nucleus=mvb.
At the point of minimum distance (s) form the nucleus, velocity v' of the projectile is normal to the radius vector (form the centre of nucleus to projectile) , fig.
`:. ` Angular momentum to projectile about the nucleus =mv's
According to the law of conservation of angular momentum

`mv's=mvb or v'=(vb)/s....(i)`
Now, at infinity, K.E. of particle =`1/2 mv^2`
and P.E.=0
At the minimum distance s, K.E of particle =`1/2mv'^2`
P.E of particle `=1/(4pi in_0) ((Ze)(Z'e))/s`
According to the principle of energy conservation,
`1/2mv'^2+1/(4pi in_0) (Z Z'e^2)/s=1/2 mv^2`
Using (1) we get,
`1/2mv^2 (b^2)/(s^2)+1/(4pi in_0) (Z Z'e^2)/s=1/2mv^2`
or `1/2mv^(2)b^(2)+1/(4pi in_0) Z Z'e^2.s=1/2mv^2s^2`
Dividing both sides by `(1/2mv^2)`, we get,
`b^2+1/(2pi in_0) (Z Z'e^2 s)/(mv^2)=s^2`
for a head on collision, b=0
`:. s^2=1/(2pi in_0) (Z Z'e^2 s)/(mv^2)`
or `s=1/(2pi in_0) (Z Z'e^2)/(mv^2)=1/(4pi in_0) ((Ze)(Z'e))/((1/2 mv^2))`
Which is `r_0`, the distance of closest approach.
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
A particle of mass m, charge q gt 0 and initial kinetic energy K is projected from infinity towards a heavy nucleus of charge Q assumed to have a fixed position. (a) If the aim is perfect, how close to the centre of the nucleus is the particle when it comes instantaneously to rest ? (b) With a particular imperfect aim, the particle's closest approach to nucleus is twicw the distance determined in (a). Determine speed of particle at the closest distance of approach.
When an a-particle of mass 'm' moving with velocity 'v' bombards on a heavy nucleus of charge 'Ze', its distance of closest approach from the nucleus depends on v as:
When an alpha particle of mass m moving with velocity v bombards on a heavy nucleus of charge Ze, its distance of closest approach form the nucleus depends on m as
When an alpha- particle of mass 'm' moving with velocity 'v' bombards on a heavy nucleus of charge 'Ze' its distance of closest approach from the nucleus depends on m as :
A particle of mass m is moving along the line y=b,z=0 with constnat speed v . State whether the angular momentum of particle about origin is increasing. Decreasing or constant.
Figure shows a charge +Q clamped at a point in free space. From a large distance another charge particle of charge -q an.d mass m is thrown toward +Q with an impact parameter d as shown with speed v. Find the distance of closest approach of the two particles.
for scattering by an inverse square law field (such as that produced by a charged nucleus in Rutherford's model), the relation between impact parameter b and the scattering angle theta is given by b=(Ze^2 cot theta//2)/(4pi in_0(1/2mv^2)) (a) What is the scattering angle for b=0? (b) for given impact parameter, b, does the angle of deflection increase or decrease with increase in energy? (c) What is the impact parameter at which the scattering angle is 90^@ for Z=79 and initial energy=10MeV? (d) Why is it that the mass of the nucleus does not enter the formula above, but its charge does? (e) for a given energy of the projectile, does the scattering angle increase or decrease with decrease in impact parameter?
A long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x_0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.