Home
Class 12
PHYSICS
A double ionised lithium atom is hydroge...

A double ionised lithium atom is hydrogen like with atomic number `3`
(i)Find the wavelength of the radiation to excite the electron in `Li^(++)`from the first to the third bohr orbit (lonisation energy of the hydrogen atom equals `13. 6eV`
(ii) How many spectral lines are observed in the emission spectrum of the above excited system ?

Text Solution

Verified by Experts

In the nth orbit of hydrogen atom, energy of electron, `E_(n)=(-13.6)/(n^(2))eV`
In case of hydrogen like atom, the energy is `E_(n)'=3^(2)(E_(n))=(-9xx13.6)/(n^(2))eV`
for n=1, `E_(1)'=-9xx13.6eV`,
for n=3, `E_(3)'=(-9xx13.6)/(3^(2))=-13.6 eV`
Energy of photon required to excite the electron form n=1 to n=3 is
`hv=E_(3)'-E_(1)'=-13.6-(-9xx13.6)=8xx13.6eV`
`(hc)/lambda=8xx13.6xx1.6xx10^(-19)("joule")`
`lambda=(hc)/(8xx13.6xx1.6xx10^(-19))=(6.63xx10^(-34)xx3xx10^(8))/(8xx13.6xx1.6xx10^(-19))=114.25xx10^(-10)m=114.25Å`
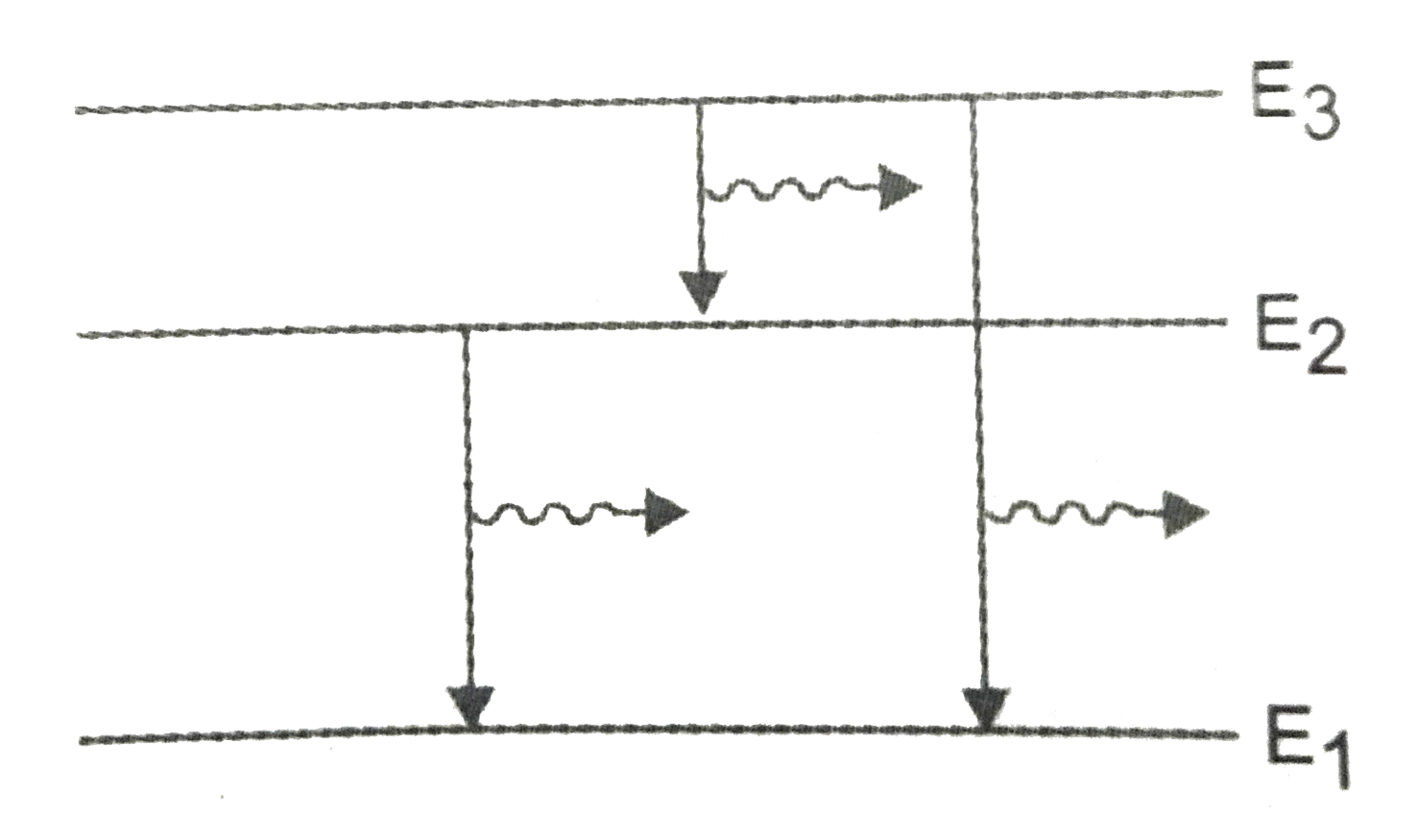
This is the wavelength of the radiation requirede. The possible spectral lines observed in this system are three : `E_(3)toE_(1),E_(3)toE_(2) and E_(2)toE_(1)` as shown in fig.
Promotional Banner

Topper's Solved these Questions

  • ATOMS AND NUCLEI

    PRADEEP|Exercise (II) very short answer 16|1 Videos

  • ATOMS AND NUCLEI

    PRADEEP|Exercise (I) Short Answer questions 1|1 Videos

  • COMMUNICATION SYSTEMS

    PRADEEP|Exercise MODEL TEST PAPER-2|9 Videos

Similar Questions

Explore conceptually related problems

A double ionised lithium atom is hydrogen like with atomic number 3 (i)Find the wavelength of the radiation to excite the electron in Li^(++) from the first to the third bohr orbit (lonisection energy of the hydrogen atom equals 13. 6) (ii) How many spectral lines are observed in the emission spetrum of the above excled system ?

A doubly ionized lithium atom is hydrogen like with atomic number 3. Find the wavelength of the radiation required to excite the electron in Li^(++) from to the third Bohr orbit (ionization energy of the hydrogen atom equals 13.6 eV).

A doubly ionized lithium atom is hydrogen like with atomic . number 3. Find the wavelength of the radiation to excite the electron in . Li++ form the first to the third Bohr orbit. The ionization energy of the hydrogen . Atom is 13.6V.

Consider a gas consisting Li^(+2) (which is hydrogen like ion). (a) Find the wavelength of radiation required to excite the electron in Li^(++) from n=1 and n=3 . (Ionisation energy of the hydrogen atom equals 13.6 eV ). (b) How many spectral lines are observed in the emission spectrum of the above excited system?

A double charged lithium atom is equivalent to hydrogen whose atomic numer is 3 . The wavelength of required radiation for emitted electron from first to third Bohr orbit in Li^(++ will be (lonisation energy of hydrogen atom is 13.6 eV )

A doubly ionized lithium atom is hydrogen like with atomic number 3 . Find the electron in (Li^(+ +)) from the first to thired Bohr orbit . The ionization energy of the hydrogen atom is 13.6 eV .

(a)Find the wavelength of the radiation required to excited the electron is Li^(++) from the first to the third Bohr orbit (b) How many speciral are obseved in the emission apactrum of the above excited system?