लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
शंकु परिच्छेदः वृत
BALAJI PUBLICATION|Exercise अभ्यास प्रश्न 15.1|27 Videosशंकु परिच्छेदः वृत
BALAJI PUBLICATION|Exercise अभ्यास प्रश्न 15.2|11 Videosशंकु परिच्छेदः अतिपरवलय
BALAJI PUBLICATION|Exercise स्वमूल्यांकन परीक्षण ((B) विवेचनात्मक सोच वाले प्रश्न )|1 Videosसमकोणीय कार्तीय निर्देशांक निकाय
BALAJI PUBLICATION|Exercise विवेचनात्मक सोच वाले प्रश्न|4 Videos
BALAJI PUBLICATION-शंकु परिच्छेदः वृत-स्वमूल्यांकन परीक्षण ((B) विवेचनात्मक सोच वाले प्रश्न )
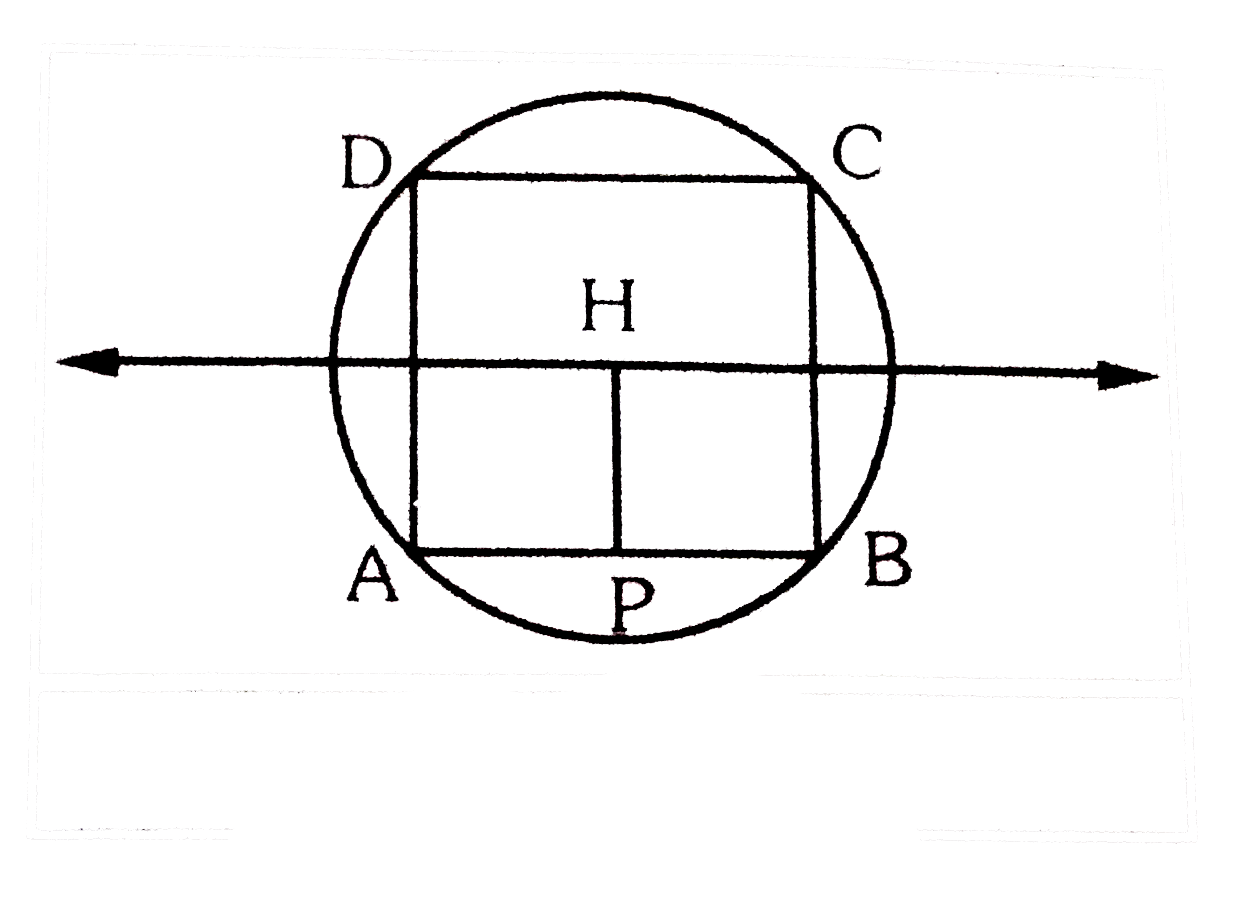
- आयत ABCD के परिवृत्त के व्यास का समीकरण 4y=x+7 है। यदि A तथा B क्रमशः ...
Text Solution
|
- सिद्ध कीजिए की तीन वृतों x^(2)+y^(2)-4x-6y-12=0," "x^(2)+y^(2)+2x+4y...
Text Solution
|
- सिद्ध कीजिए की वृत x^(2)+y^(2)+2gx+2 fy+c=0 में बने एक समबाहु त्रिभुज ...
Text Solution
|
- t के सभी वास्तविक मानों के लिए, -1 le t le 1, a in R सिद्ध कीजिए की बि...
Text Solution
|