लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
शंकु परिच्छेद : परवलय
BALAJI PUBLICATION|Exercise अभ्यास प्रश्न 16.1|30 Videosशंकु परिच्छेद : परवलय
BALAJI PUBLICATION|Exercise अभ्यास प्रश्न 16.2|1 Videosरैखिक असमिकाएँ
BALAJI PUBLICATION|Exercise स्वमूल्यांकन परीक्षण ((B) विवेचनात्मक सोच वाले प्रश्न)|13 Videosशंकु परच्छेद: दीर्घवृत्त
BALAJI PUBLICATION|Exercise स्वमूल्यांकन परीक्षण|19 Videos
BALAJI PUBLICATION-शंकु परिच्छेद : परवलय -स्वमूल्यांकन परीक्षण ((B) विवेचनात्मक सोच वाले प्रश्न )
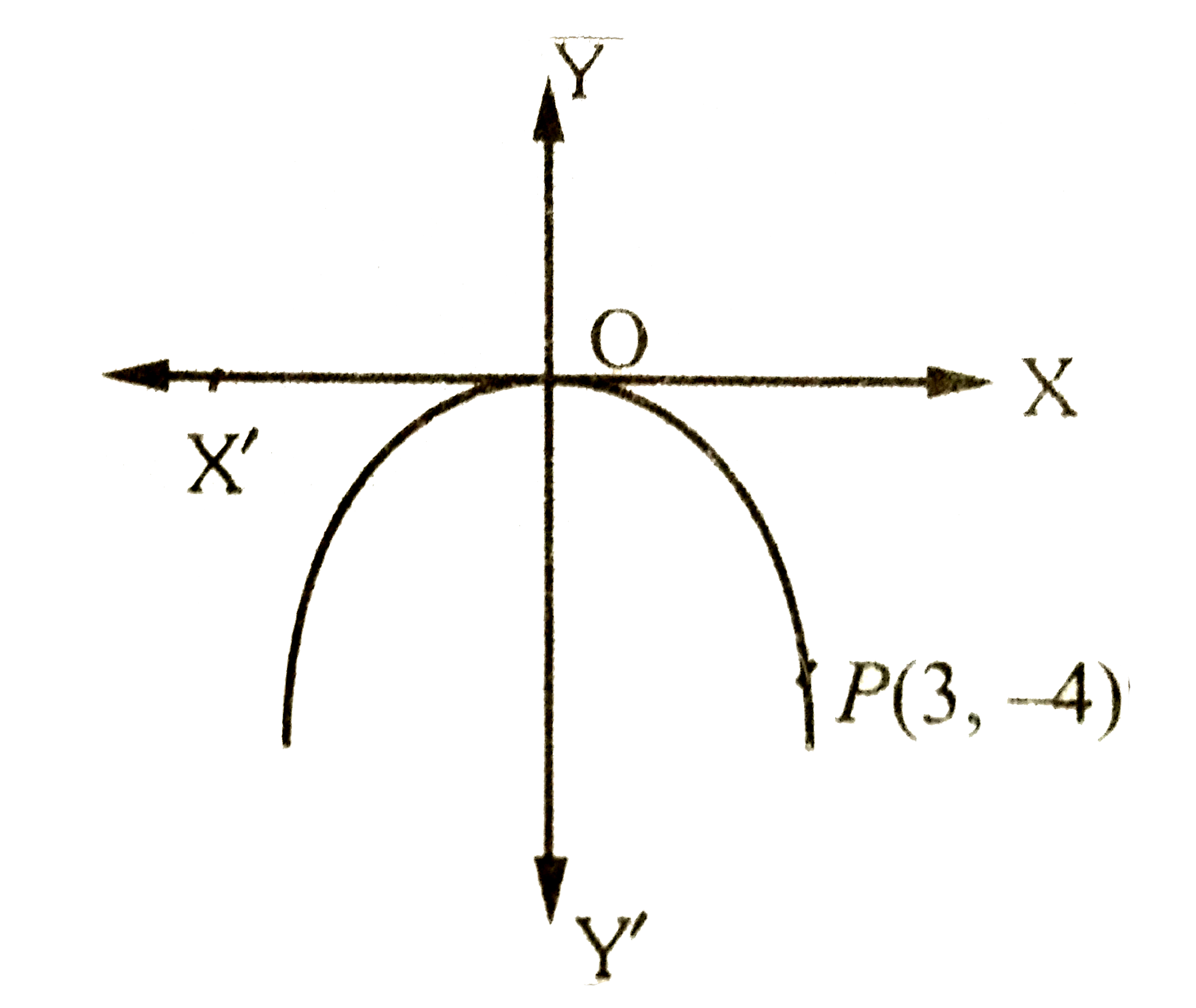
- बिन्दु P(3,-4) से होकर जाने वाले तथा y -अक्ष के सममित उस परवलय...
Text Solution
|
- माना PQ , परवलय y^(2) = 4ax कि नाभीय जीवा है , P व Q पर परवलय की स्...
Text Solution
|
- प्रश्न 11 में यदि जीवा PQ , परवलय के शीर्ष पर theta कोण अन्तरित ...
Text Solution
|
- दर्शाइये कि दोनों परवलयो y^(2) = 4x तथा x^(2) = - 32y को स्पर्श ...
Text Solution
|
- माना O शीर्ष है तथा a परवलय x^(2) = 8y पर कोई बिन्दु है | यदि बि...
Text Solution
|
- माना a,r,s,t शून्यक वास्तविक सख्याए है , माना P(at^(2), 2at)Q,R(ar...
Text Solution
|
- प्रश्न (15) में , यदि st =1 , हो तब परवलय के बिन्दु P पर स्पर्शी ...
Text Solution
|