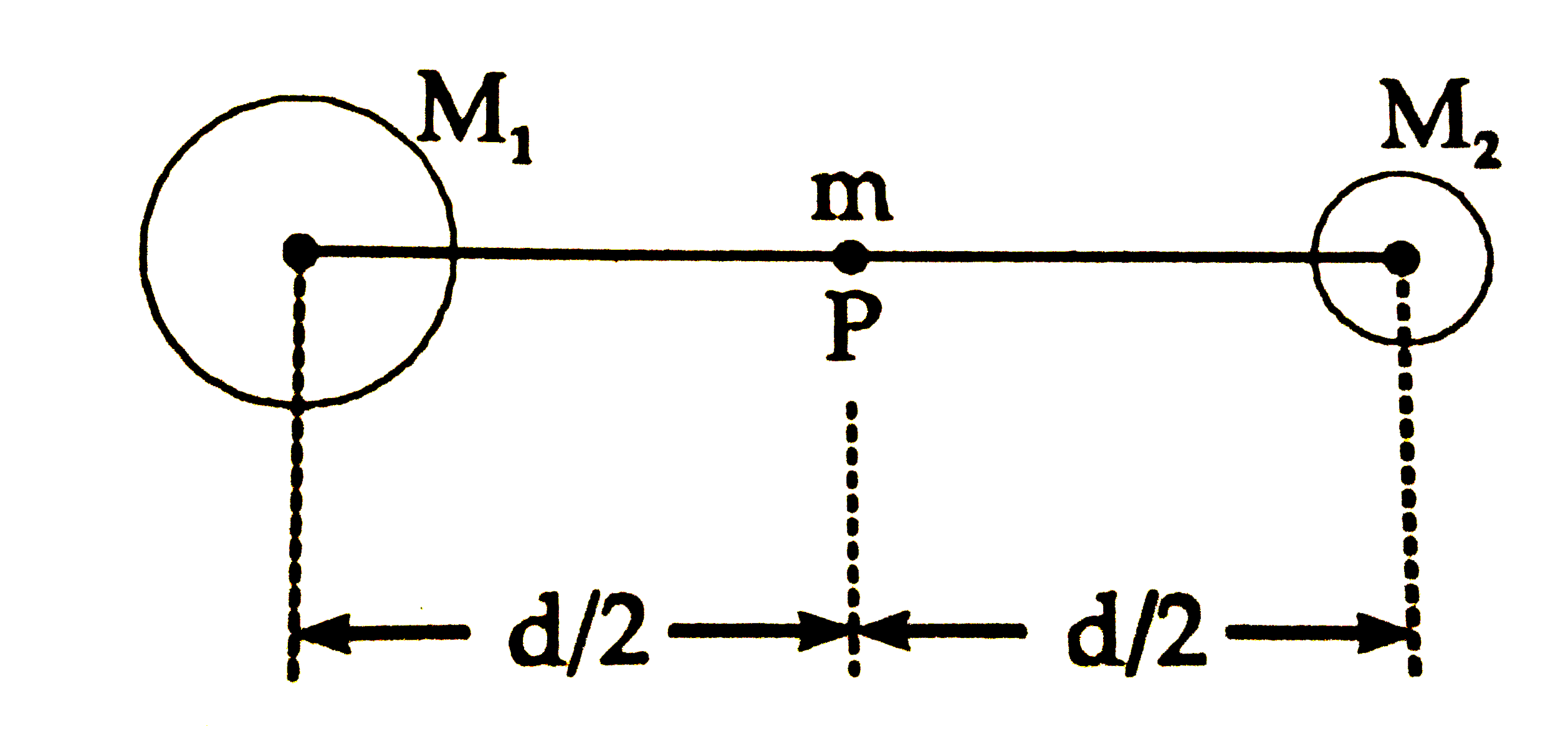
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NIKITA PUBLICATION-GRAVITATION-Multiple Choice Questions
- The acceleration due to gravity on the surface of the moon is one-sixt...
Text Solution
|
- The velocity with which a body should be projected from the surface of...
Text Solution
|
- The masses and radii of the earth an moon are M(1) and R(1) and M(2), ...
Text Solution
|
- The escape velocity of the earth is 11.2 km/s. For a planet whose mass...
Text Solution
|
- A satellite orbiting close to earth surface will escape, if
Text Solution
|
- The escape velocity corresponding to a planet of mass M and radius R i...
Text Solution
|
- The escape Velocity from the earth is 11.2 Km//s. The escape Velocity ...
Text Solution
|
- If the acceleration due to gravity at the surface of the earth is g, t...
Text Solution
|
- A projectile is fired from the surface of earth of radius R with a vel...
Text Solution
|
- The escape velocity from the surface of the earth of radius R and dens...
Text Solution
|
- The radius of a planet is 1/4 of earth’s radius and its acceleration d...
Text Solution
|
- The escape velocity of a body from the earth is V(e). The escape veloc...
Text Solution
|
- The radius of the earth is reduced by 1% with mass remaining the same....
Text Solution
|
- If M be the mass of the earth, R its radius (assumed spherical) and G ...
Text Solution
|
- An artificial satellite is moving in a circular orbit around the earth...
Text Solution
|
- A body is projected vertically upwards from the surface of the earth w...
Text Solution
|
- The escape velocity for a rocket from earth is 11.2 km / sec . Its val...
Text Solution
|
- The escape velocity from the earth is about 11 km/s. The escape veloci...
Text Solution
|
- The escape velocity from the surface of earth is V(e). The escape velo...
Text Solution
|
- The escape velocity for the earth is 11.2 km / sec . The mass of anoth...
Text Solution
|