Topper's Solved these Questions
SIMILARITY
CHETAN PUBLICATION|Exercise Practice Set - 1.4|7 VideosSIMILARITY
CHETAN PUBLICATION|Exercise Problem Set - 1|12 VideosSIMILARITY
CHETAN PUBLICATION|Exercise Practice Set - 1.2|13 VideosQUADRATIC EQUATIONS
CHETAN PUBLICATION|Exercise ASSIGNMENT|12 VideosSTANDARD IX SYLLABUS
CHETAN PUBLICATION|Exercise PROBLEMS FOR PRACTICE|20 Videos
Similar Questions
Explore conceptually related problems
CHETAN PUBLICATION-SIMILARITY -Practice Set - 1.3
- As shown in adjoining figure , two poles of height 8 m and 4 mare perp...
Text Solution
|
- Are the triangles in the figure given similar ?
Text Solution
|
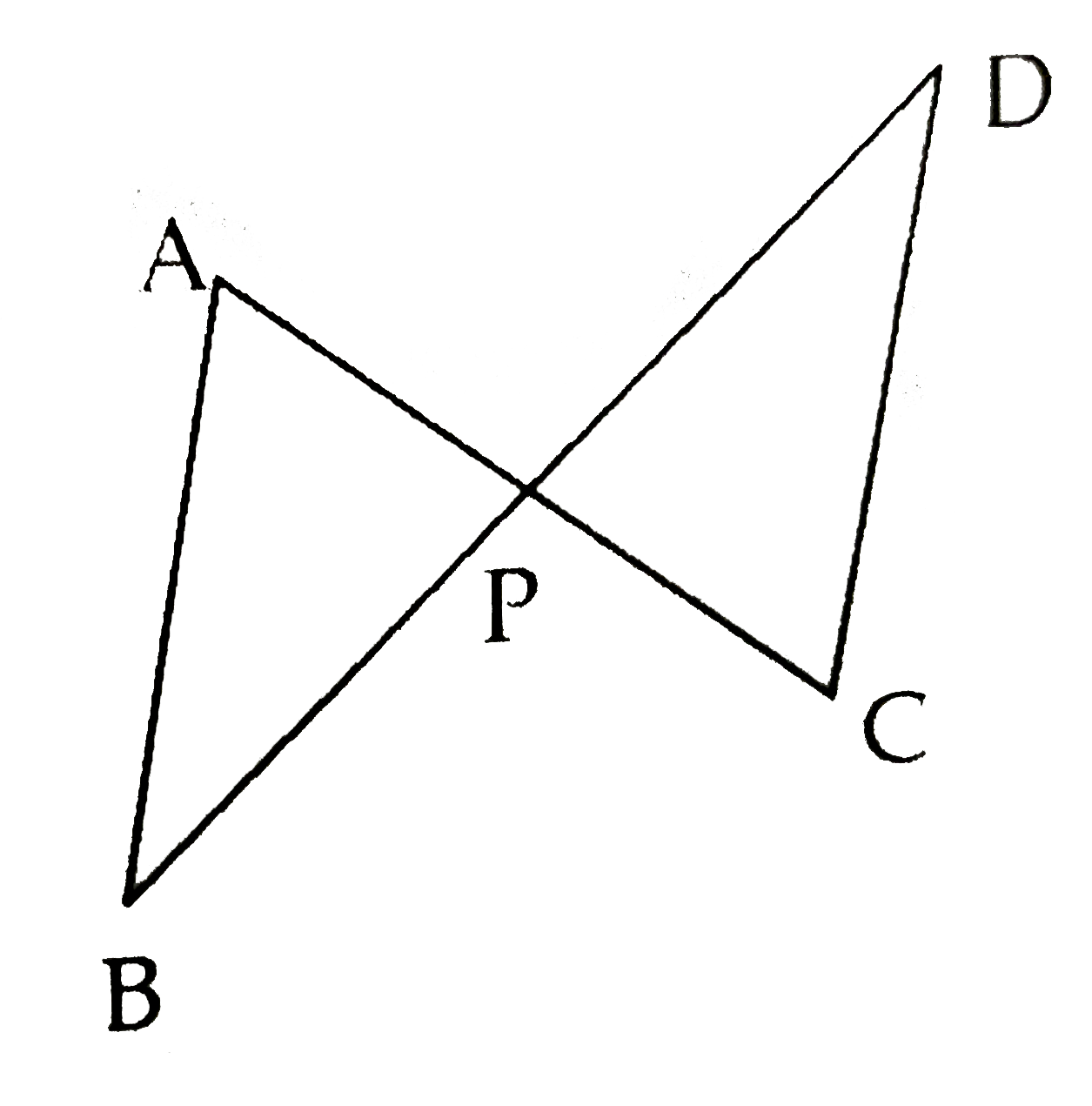
- In the figure seg AC and seg BD intersects each other at point P and ...
Text Solution
|
- In trapezium PQRS , side PQ|| side SR. AR= 5 AP and AS = 5AQ. Prove t...
Text Solution
|
- In adjoining figure, angleABC=75^(@),angleEDC=75^(@) state which two ...
Text Solution
|
- squareABCD is a parallelogram. Point E is on side BC , line DE interse...
Text Solution
|
- In trapezium ABCD , side AB||DC Diagonals AC and BD intersect in O . I...
Text Solution
|
- In DeltaABC,APbotBC,BQbotAC,B-P-C,A-Q-C "then prove that " DeltaCPA~De...
Text Solution
|
- In the figure , in DeltaABC , point D on side BC is such that , Delta...
Text Solution
|