Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SIMILARITY
CHETAN PUBLICATION|Exercise Problem Set - 1 (MCQs)|16 VideosSIMILARITY
CHETAN PUBLICATION|Exercise PROBLEMS FOR PRACTICE|30 VideosSIMILARITY
CHETAN PUBLICATION|Exercise Practice Set - 1.4|7 VideosQUADRATIC EQUATIONS
CHETAN PUBLICATION|Exercise ASSIGNMENT|12 VideosSTANDARD IX SYLLABUS
CHETAN PUBLICATION|Exercise PROBLEMS FOR PRACTICE|20 Videos
Similar Questions
Explore conceptually related problems
CHETAN PUBLICATION-SIMILARITY -Problem Set - 1
- In DeltaABC,B-D-CandBD=7,BC=20 Then find the following ratio. (A(D...
Text Solution
|
- In DeltaABC,B-D-CandBD=7,BC=20 Then find the following ratio. (A(D...
Text Solution
|
- In DeltaABC,B-D-CandBD=7,BC=20 Then find the following ratio. (A(D...
Text Solution
|
- Ratio of areas of two triangles with equal height is 2: 3 . If base o...
Text Solution
|
- In the figure given angleABC=angleDCB=90^(@). AB=6,DC=8. "then" (A(Del...
Text Solution
|
- In the adjoining figure , PM=10"cm"A(DeltaPQS)=100" sq cm" A(DeltaQRS)...
Text Solution
|
- In the figure A-D-C and B-E-C. "seg "DE||"side " AB. "if " AD=5, DC=3,...
Text Solution
|
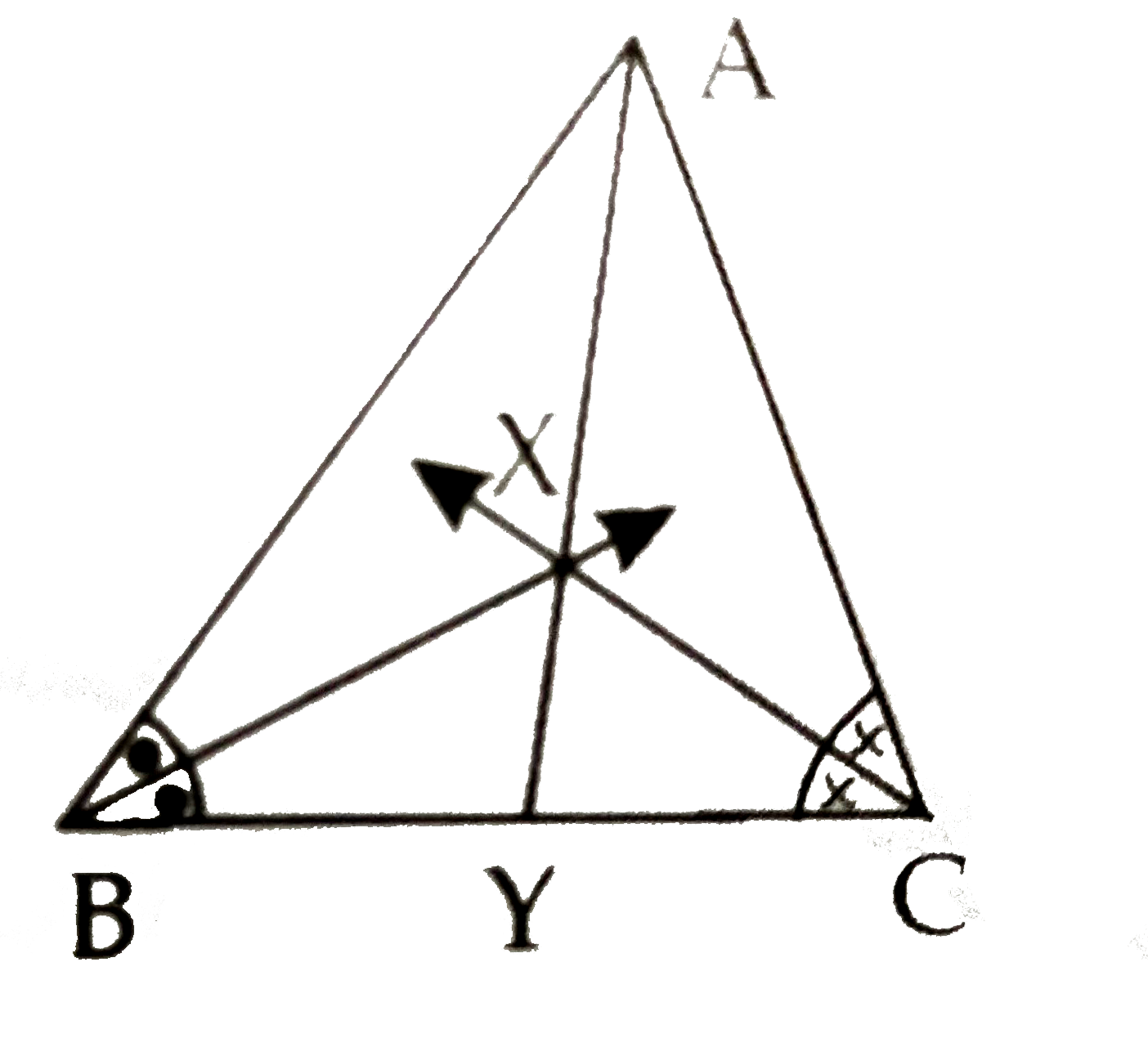
- In the adjoining figure bisectors of angleBand angleC intersect each ...
Text Solution
|
- In the figure given seg PA, seg QB, seg RC and seg SD are perpendicula...
Text Solution
|
- In squareABCD, "seg " AD||"seg " BC. Diagonal AC and diagonal BC inte...
Text Solution
|
- In the adjoining figure , XY || seg AC . If 2AX = 3 xxBX and XY=9. Co...
Text Solution
|
- DeltaMNT~DeltaQRS : Length of altitude drawn from vertex T is 5 and le...
Text Solution
|