Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CIRCLE
CHETAN PUBLICATION|Exercise Assignment - 3 ((A) Solve the following sub questions ):|1 VideosCIRCLE
CHETAN PUBLICATION|Exercise Assignment - 3 ((B) Solve any one of the following questions ):|1 VideosCIRCLE
CHETAN PUBLICATION|Exercise Problems for practice (Based on parctice Set 3.4)|7 VideosCHALLENGING QUESTIONS
CHETAN PUBLICATION|Exercise Mensuration|9 VideosCO-ORDINATE GEOMETRY
CHETAN PUBLICATION|Exercise ASSIGNMENT-5|11 Videos
Similar Questions
Explore conceptually related problems
CHETAN PUBLICATION-CIRCLE-Problems for practice (Based on parctice Set 3.5)
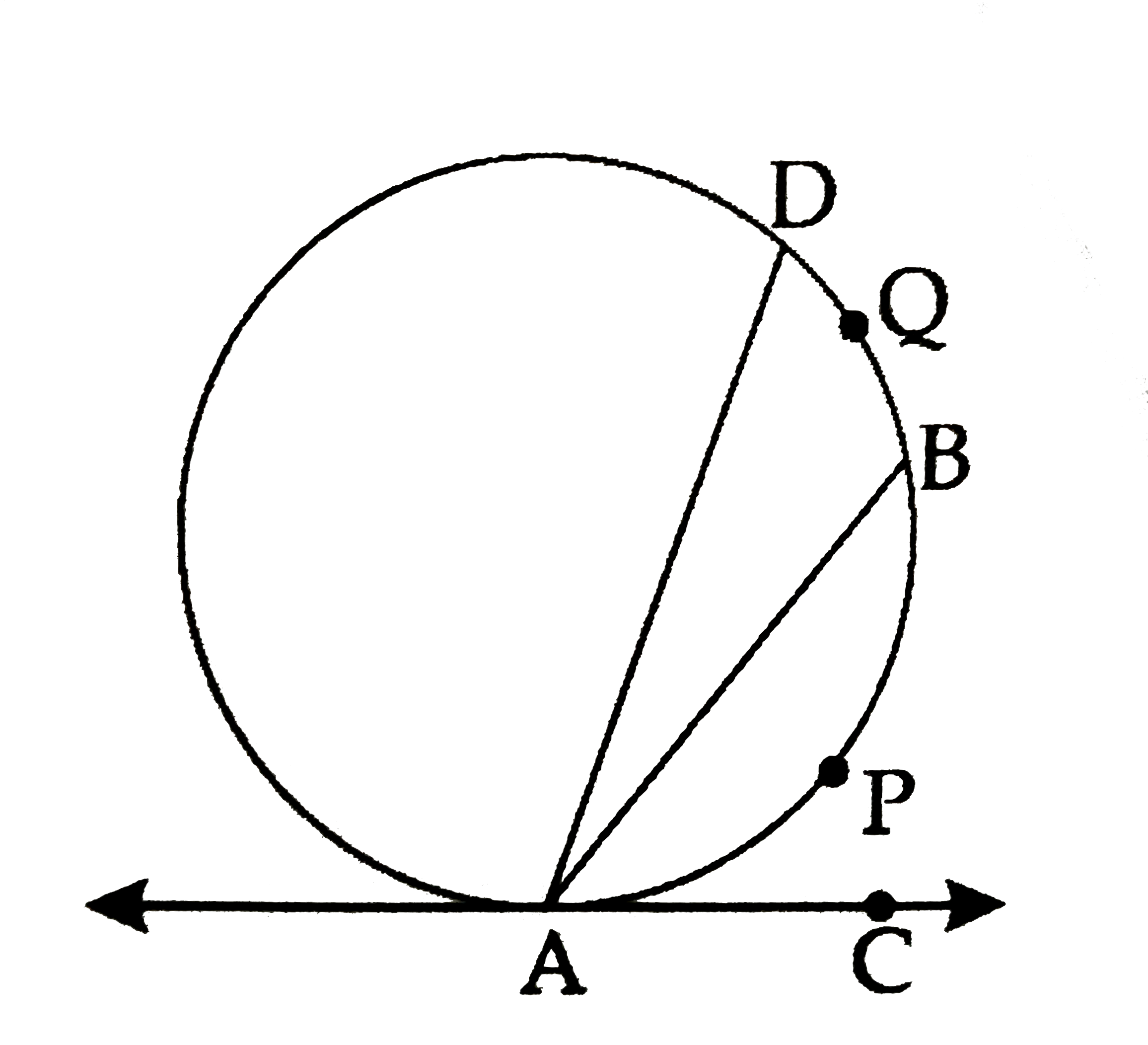
- Seg AB and seg AD are the chords of the circle . C is a point on tang...
Text Solution
|
- Secant AC and secnat AE intersects in point A . Points of intersection...
Text Solution
|
- In the adjoining figure line PA is tangent at point A . Line PBC is a ...
Text Solution
|
- squareABCD is a rectangle. Taking AD as a diameter, a simicircle AXD i...
Text Solution
|
- In the adjoining figure point O is the centre of the circle . Line PB...
Text Solution
|