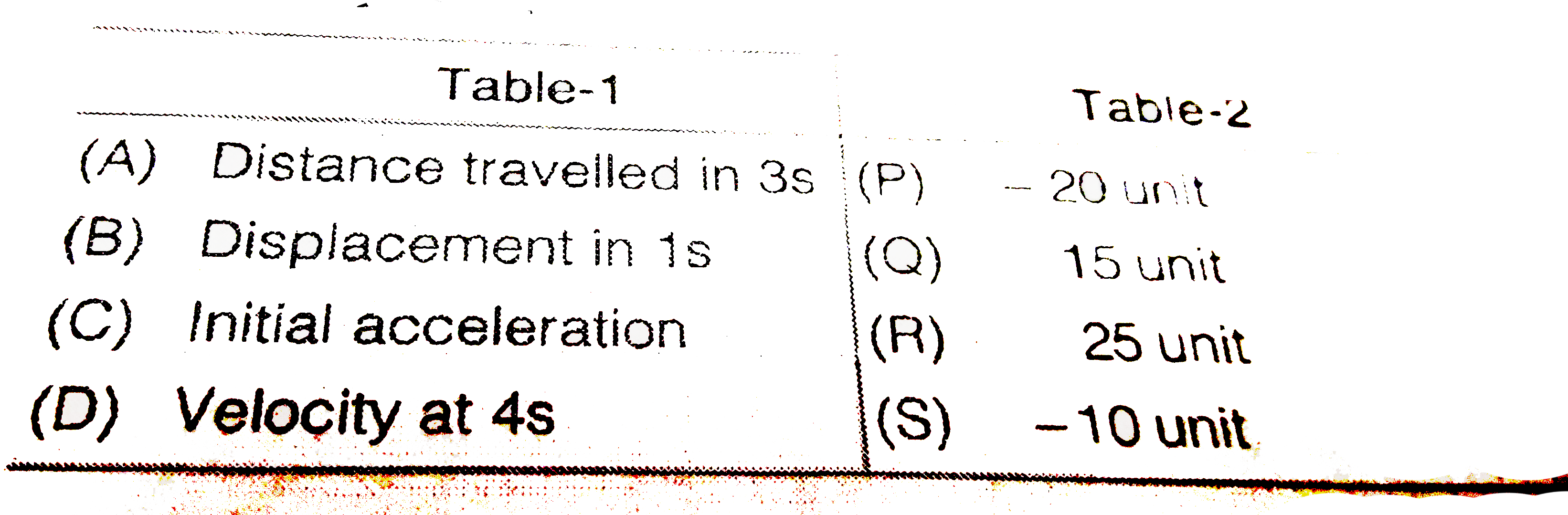Similar Questions
Explore conceptually related problems
Recommended Questions
- In the s-t equations (s=10+20t-5t^(2)) match the following
Text Solution
|
- In the s-t equations (s=10+20t-5t^(2)) match the following
Text Solution
|
- Given s=t^(2)+5t+3, find (ds)/(dt)
Text Solution
|
- The displacment of a particle is represented by the following equation...
Text Solution
|
- The displacement s of an object is given as a function of time t by th...
Text Solution
|
- सरल रेखीय गति में एक वस्तु कि स्थिति (s ) का समय (t ) के साथ परिवर्तन ...
Text Solution
|
- If displacement S at time t is S=10t-5t^(2), then velocity at time t i...
Text Solution
|
- If S=t^(4)-5t^(2)+8t-3, then initial velocity of the particle is
Text Solution
|
- If 3s+5t=10, and 2s-t=7, what is the value of (1)/(2^(s))+3t ?
Text Solution
|