Home
Class 12
PHYSICS
A bullet of mass m and charge q is fired...

A bullet of mass m and charge `q` is fired towards a solid unifromly charged sphere of redius `R ` and total cbharge ` + q`. If it strikes the surface of sphere with speed `u`, find the minimum speeed `u` so that it can penetrate through the sphere , (Neglect all resistance forces or friction acting on bullet except electrositatic forces )
.

A

`(q)/(sqrt(2 pi varepsilon_(0)mR)`

B

`(q)/(sqrt(4 pi varepsilon_(0)mR)`

C

`(q)/(sqrt(8 pi varepsilon_(0)mR)`

D

`(sq)rt3q/(sqrt(4 pi varepsilon_(0)mR)`

Text Solution

Verified by Experts

The correct Answer is:
B
` v_s` = Potential at surfce `= 1/ (4 pi in_0 ) q/R`
` V_("in") = (KQ(3R^2-r^2))/(2R^3)`
`V_0 = 3/2 1/(4 pi in_0 ) q/R`
To pentrate it must reach cenyre of sphere.
From energy conservation
`1/2 mu^2 _ 1/ ( 4 pi in_0 ) (q.q)/R =0 + 3/2 . 1/( 4 pi in _0 ), (qq)/R`
` 1/2 mu^2 = 1/2 1/(4 pi in_0 ) q^2/R , E= (mg)/(2q)`
`u^2 = q^2 /(4 pi in_0 mR)`
`u = q/sqrt (4 pi in_0 mR)`.
Promotional Banner

Similar Questions

Explore conceptually related problems

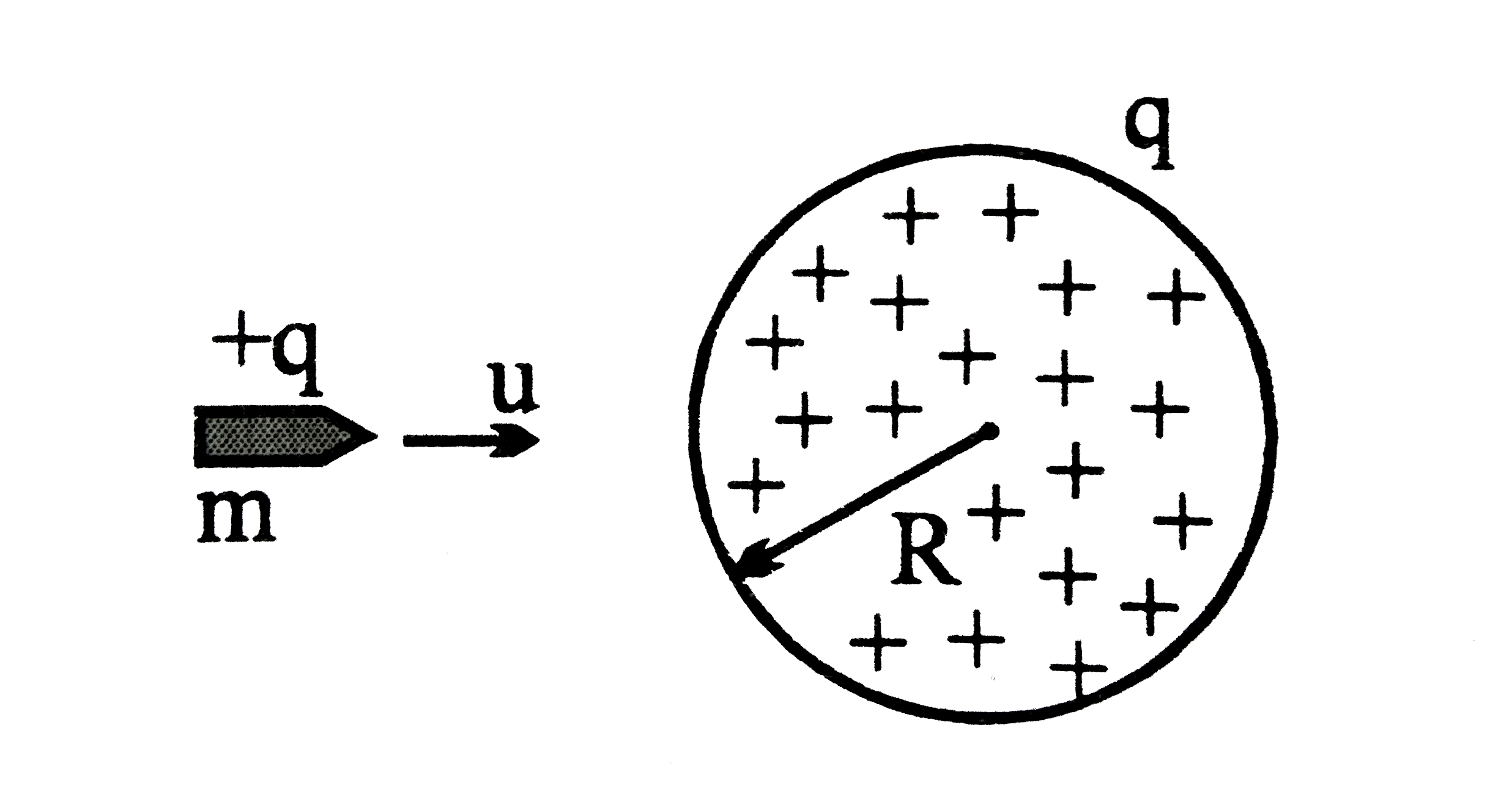
A bullet of mass m and charge q is fired towards a solid uniformly charge sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum value of u so that it can penetrate through the sphere. (Neglect all resistance force or friction acting on bullet except electrostatic forces)

A particle of mass m and charge -q moves along a diameter of a uniformluy charged sphere of radinus R and carrying a total charge +Q . Find the frequency of S.H.M. of the particle if the amplitude does not exceed .

A positive charge Q is uniformly distributed throughout the volume of a dielectric sphere of radius R. A point mass having charge +q and mass m is fired toward the center of the sphere with velocity v from a point at distance r (r gt R) from the center of the sphere. Find the minimum velocity v so that it can penetrate (R//2) distance of the sphere. Neglect any resistance other than electric interaction. Charge on the small mass remains constant throughout the motion.

In a solid uniformly charged sphere of total charge Q and radius R, if energy stored out side the sphere is U_(0) joules then find out self energy of sphere in term of U_(0) ?

A particle of mass m and charge -q moves diametrically through a uniformily charged sphere of radius R with total charge Q. The angular frequency of the particle's simple harminic motion, if its amplitude lt R, is given by

Figure shows a uniformly charged sphere of radius R and total charge Q. A point charge q is situated outside the sphere at a distance r from centre of sphere. Find out the following : (i) Force acting on the point charge q due to the sphere. (ii) Force acting on the sphere due to the point charge.

A uniformly charged sphere has radius R and charge Q on it. A negatively charged particle having mass m and charge – q shoots out of the surface of the sphere with speed V. The minimum speed (V_0) for which the particle escapes the attraction of the sphere may be called as escape speed. Will the value of V_0 depend on magnitude of q? [Recall that escape speed of a body from the surface of the earth does not depend on its mass].

A solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is

A charge +Q is uniformly distributed in a spherical volume of radius R. A particle of charge +q and mass m projected with velocity v_0 the surface of the sherical volume to its centre inside a smooth tunnel dug across the sphere. The minimum value of v_0 such tht it just reaches the centre (assume that thee is no resistance on the particle except electrostatic force) of he sphericle volume is