Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
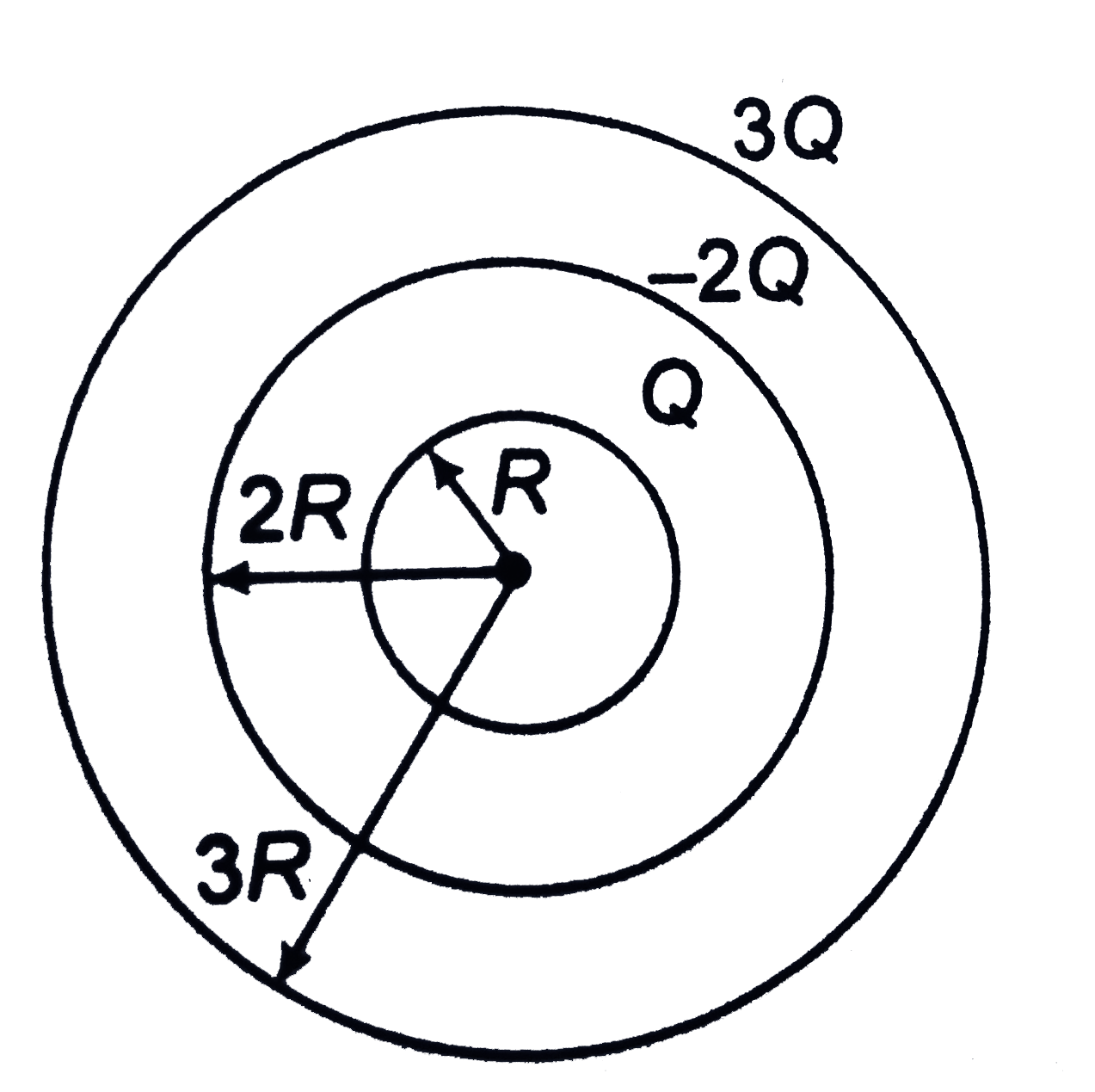
- Three concentric conducting spherical shells of radii R, 2R and 3R car...
Text Solution
|
- Three spherical shells have radii R,2R and 3R respectively. Total char...
Text Solution
|
- Three concentric conducting spherical shells of radii R, 2R and 3R car...
Text Solution
|
- Two concentric spherical conducting shells of radii R and 2R carry cha...
Text Solution
|
- A point charge q is placed inside a conducting spherical shell of inne...
Text Solution
|
- Two concentric spherical conducting shells of radii r and R (r lt R ) ...
Text Solution
|
- If a thin spherical shell of radius r and charge q is kept inside a th...
Text Solution
|
- Three concentric conducting spherical shells of radii R, R2 and 3R car...
Text Solution
|
- A solid metal sphere of radius R has a charg +2Q. A hollow spherical s...
Text Solution
|