Home
Class 12
PHYSICS
Two thin wire rings each having radius R...

Two thin wire rings each having radius R are placed at distance d apart with their axes coinciding. The charges on the two are `+Q` and `-Q`. The potential difference between the centre so the two rings is

A

zero

B

`(QR)/(4pi varepsilon_0d^2)`

C

` Q/( 4 pi varepsilon_0) [1/R - 1/(sqrt R^2 +d^2)]`

D

`(QR)/(4pi varepsilon_0d^2)`

Text Solution

Verified by Experts

The correct Answer is:
D
`V_A =` (potnyial due to chatge `+q` on ring `A 0 +` (potential due to charge ` -q` on ring `B`)
`V_A = (v+q A)`
`= 1/(4 pi varepsilon_0) (q/R - q/d_1), d_1 = sqrt (R^2 +d^2)`
`= 1/(4 pivarepsilon_0 ) q/R - q/(sqrt (R^2 +d^2))` ...(1)

Similarly,
`V_B = 1/( 4 pi varepsilon_0) (- q/R + q/(sqrt (R^2 +d^2))`
Potential difference `V_A - V_B`
` = 1/(4 pivarepsilon_0) q/R + 1/(4 pi varepsilon_0) q/R - 1/(4 pi varepsilon_0) q/(sqrt (R^2 +d^2)) - 1/(4 pi varepsilon_0) q/(sqrt (R^3 +d^2)) - 1/(4 pi varepsilon_0) q/(sqrt R^2 +d^2))`.
`= 1/(2 pi varepsilon_0) (q)/R - q/(sqrt (R^2 +d^2)`.
Promotional Banner

Similar Questions

Explore conceptually related problems

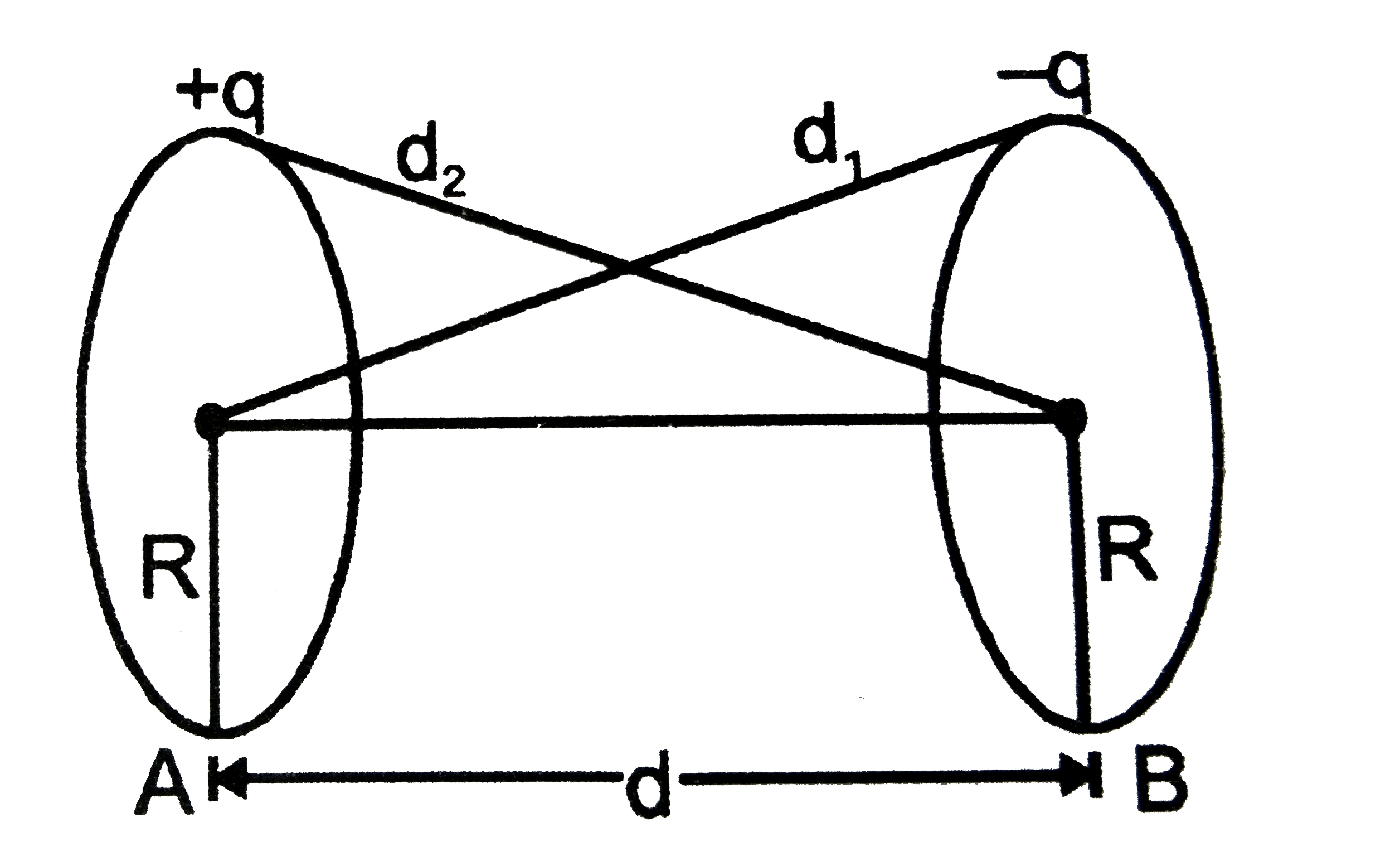
Two thin wire rings each having a radius R are placed at a distance d apart with their axes coiciding. The charges on the two rings are +q and -q . The potential difference between the centres of the two rings is

The two oppositely charged rings of radii a are seprated by s . Find the potential difference between center of the ring ?

A spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge Q(R gt r0 . The potential difference between the two is

A spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge Q (R gt r). The potential difference between the two is

Potential on the axis of ring of radius 3R and at distance 4R from centre of ring is (charge on the ring is Q )

Two point charges +q and -q are placed a distance x apart. A third charge is so placed that al the three charges are in equilibrium. Then

Two positively charged particles each having charge Q and are d distance apart. A third charge is introduced in midway on the line joining the two charges. Find the nature and magnitude of third charge so that the system is in equilibrium.