Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- An infinitely long solid cylinder of radius R has a uniform volume ch...
Text Solution
|
- An infinitely long solid cylinder of radius R has a uniform volume ch...
Text Solution
|
- A long cylinder of uniform cross section and radius R is carrying a cu...
Text Solution
|
- An infinitely long solid cylinder of radius R has a uniform volume cha...
Text Solution
|
- Inside a uniformly charged infinitely long cylinder of radius 'R' and ...
Text Solution
|
- An infinity long cylinder of radius R has an infinitely long cylindric...
Text Solution
|
- (a) There is a long uniformly charged cylinder having a volume charge ...
Text Solution
|
- A solid non-conduction cylinder of radius R is charge such that volume...
Text Solution
|
- An infinitely long solid cylinder of radius R with uniform volume char...
Text Solution
|
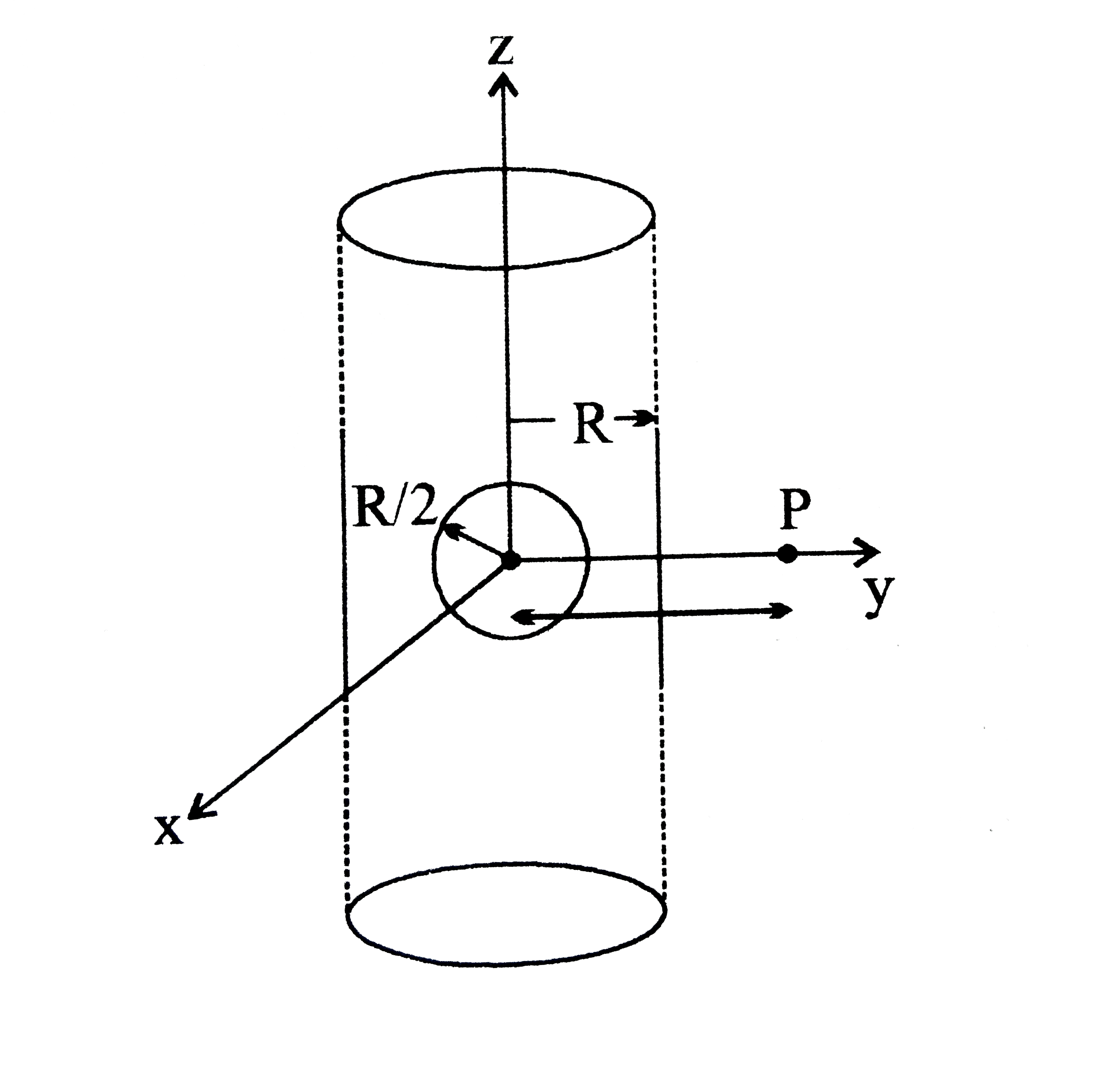 .
.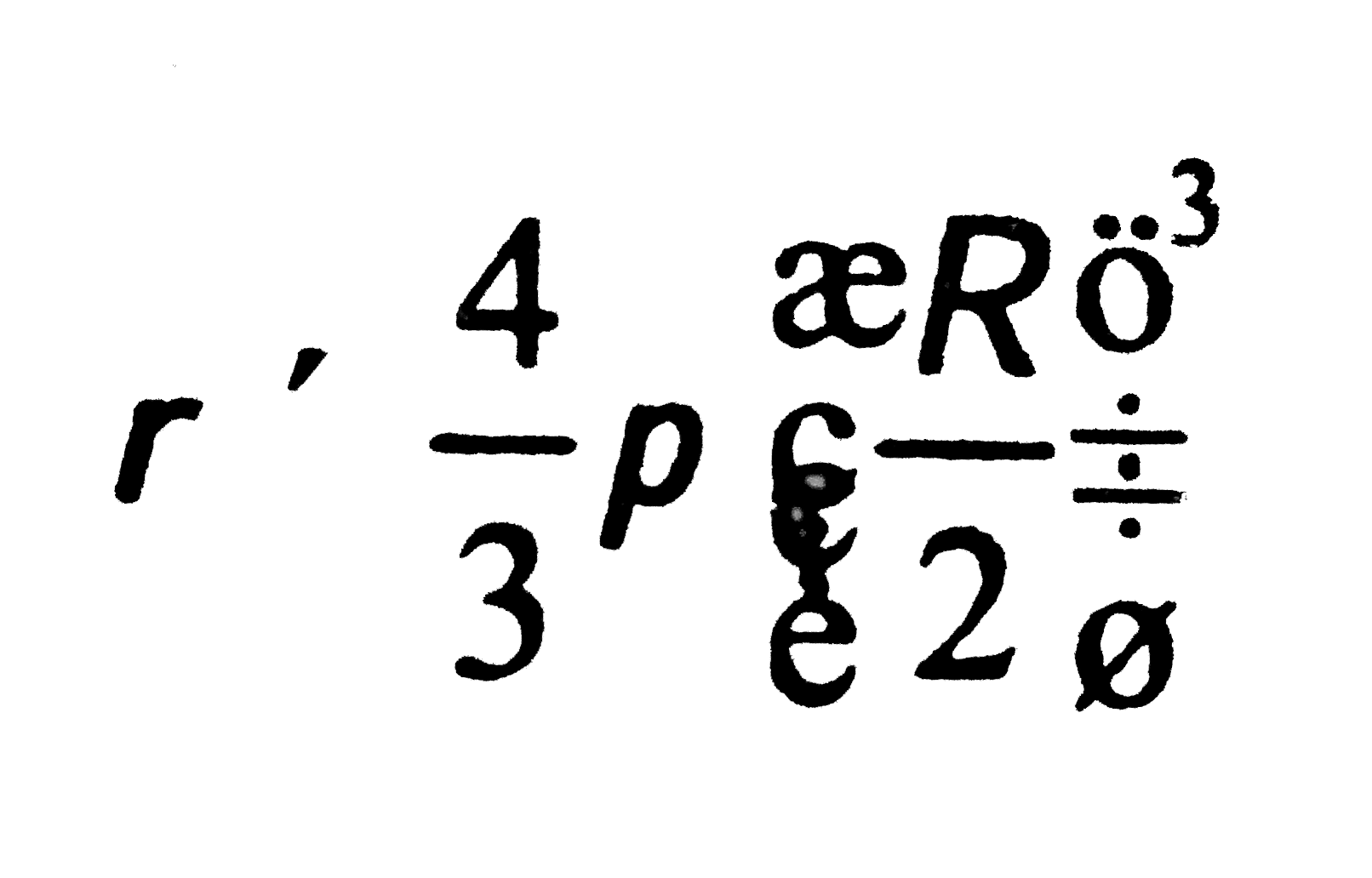 . ...(3)
. ...(3)