Home
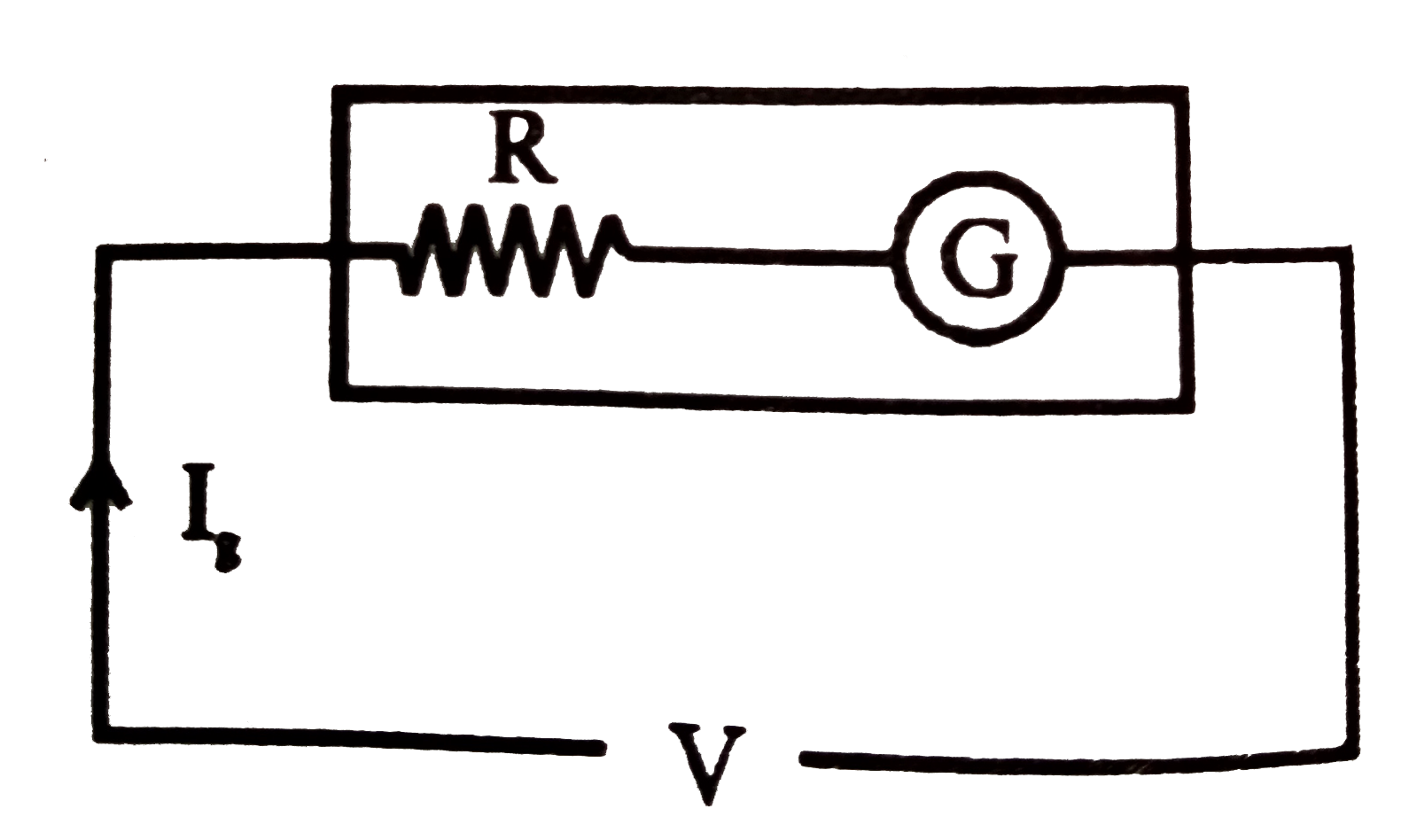
Class 12
PHYSICS
A galvanometer coil has a resistance 90 ...

A galvanometer coil has a resistance `90 Omega` and full scale deflection current `10 mA`. A `910 Omega` resistance is connected in series with the galvanometer to make a voltmeter. If the least count of the voltmeter is `0.1 V` the number of divisions on its scale is

A

`90`

B

`91`

C

`100`

D

none

Text Solution

Verified by Experts

The correct Answer is:
C
`I_(g)(R+G)=VimpliesR+G=V/I_(B)`
`R=V/(I_(g))-G`

`V=(R+G)I_(g)=(910+90)xx10mA=10`volt
`Nxx0.1=10 implies N=100`
Promotional Banner

Similar Questions

Explore conceptually related problems

A galvanometer of resistance 50 Omega gives a full scale deflection for a current 5 xx 10^(-4) A. The resistance that should be connected in series with the galvanometer to read 3 V is

A galvanometer of resistance 40 Omega gives the full scale deflection for a current of 10 m A through it. A resistance of 9960Omega is connected in series with the galvanometer coil. The mximum voltage that can be measured by the voltmeter is

A galvanometer has coil resistance 30 Omega and full deflection current of 2mA. What resistance is needed to convert it into a voltmeter of 0.2V range.

A galvanometer with a coil of resistance 50 Omega shows full-scale deflection when 10 mA current passes through it.

A galvanometer of resistance 10Omega shows full scale deflection for current 100 mA. The resistance that needs to be connected in series with the galvanometer so that it can be used to measure potential difference in the range 0-100 V is (in Ohm):

A galvanometer coil has a resistance of 50 Omega and the meter shows full scale deflection for a current of 5 mA. This galvanometer is converted into voltmeter of range 0-20 by connecting