Home
Class 12
PHYSICS
Consider a thin square sheet of side L a...

Consider a thin square sheet of side L and thickness t, made of a material of resistivity `rho`. The resistance between two opposite faces, shown by the shaded areas in the figure is

A

directely proportional to `L`

B

directely proportional to `1`

C

independent proportional of `L`

D

independent of `t`

Text Solution

Verified by Experts

The correct Answer is:
C
`R=(rhoL)/A=(rhoL)/(Lt)=rho/t` so the correct choice is (C)
Promotional Banner

Similar Questions

Explore conceptually related problems

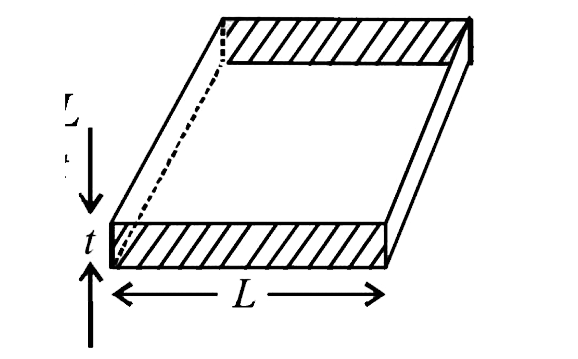
Consider a thin square sheet of side L and thicknest, made of a material of resistivity rho . The resistance between two opposite faces, shown by the shaded areas in the figure is

A wire of resistance 12 Omega m^(-1) is bent to from a complete circle of radius 10 cm . The resistance between its two diametrically opposite points, A and B as shown in the figure, is

The inductance L of a solenoid of length l , whose windings are made of material of density D and resistivity rho , is (the winding resistance is R )

A solid cylinder of length l and cross-sectional area A is made of a material whose resistivity depends on the distance r from the axis of the cylinder as rho = k//r^(2) where k is constant . The resistance of the cylinder is -

The resistance of all the wires between any two adjacent dots is R . Then, equivalent resistance between A and B as shown in figure is

Consider a wire of length l, area of cross section A, and resistivity rho with resistance 10 Omega . Its length is increased by applying a force, and it becomes four times of its original value. Find the changed resistance of the wire.

Figure 5.260 shows two square, X and Y cut from a sheet of metal of uniform thickness t. X and Y have sides of length L and 2L, respectively. The resistances R_x and R_y of the squares are measured between the opposite faces shaded in fig. What is the value of R_x//R_y?

Four conductors of same resistance connected to form a square. If the resistance between diagonally opposite corners is 8 ohm, the resistance between any two adjacent corners is