A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A thin non conducting disc of radius R is rotating clockwise (see figu...
Text Solution
|
- A charge Q is uniformly distributed over the surface of non - conducti...
Text Solution
|
- A flat dielectric disc of radius R carries an exces charge on its surf...
Text Solution
|
- A charge q is uniformly distributed on a non-conducting disc of radius...
Text Solution
|
- A non-conducting thin disc of radius R charged uniformly over one side...
Text Solution
|
- A non-conducting thin disc of radius R charged uniformly over one side...
Text Solution
|
- A thin non conducting disc of radius R is rotating clockwise (see figu...
Text Solution
|
- A non-conducting thin disc of radius R and mass m having charge unifor...
Text Solution
|
- A flat insulating disc of radius 'a' carries an excess charge on its s...
Text Solution
|
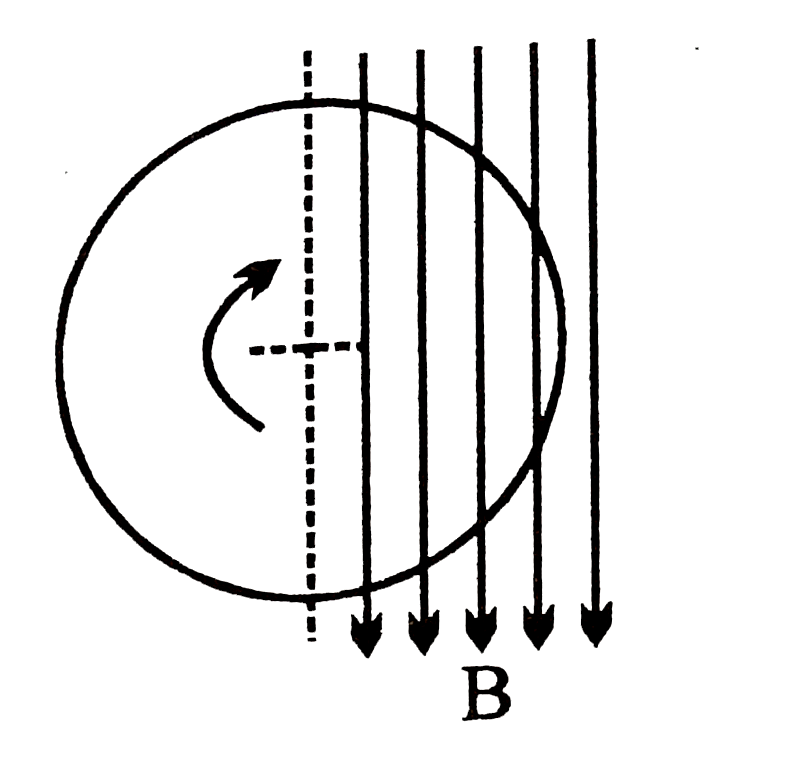 .
.