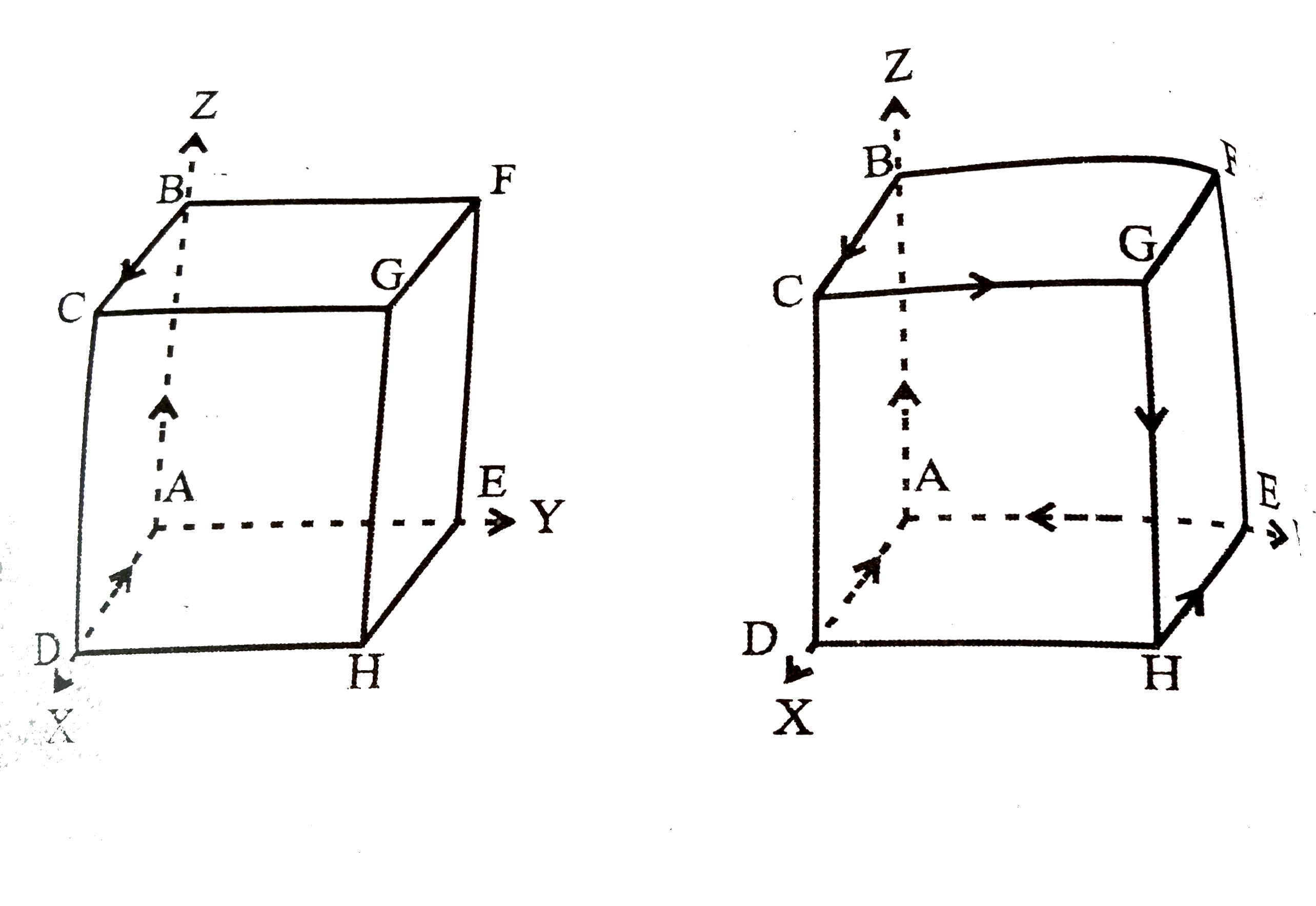
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Current I si following along the path ABCD, along the four edges of th...
Text Solution
|
- A conductor carries a constant current I along the closed path abcdefg...
Text Solution
|
- A conductor carries a constant current I along the closed path abcdefg...
Text Solution
|
- Current I flows around the wire frame along the edge of a cube as show...
Text Solution
|
- Current I si following along the path ABCD , along the four edges of t...
Text Solution
|
- A current I amperes flows through a loop abcdefgha along the edge of c...
Text Solution
|
- A current I amperes flows through a loop abcdefgha along the edge of c...
Text Solution
|
- A current I flows along a round circular loop of radius R. Find the li...
Text Solution
|
- The current is flowing along the path abcd of a cube (shown to the lef...
Text Solution
|