Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
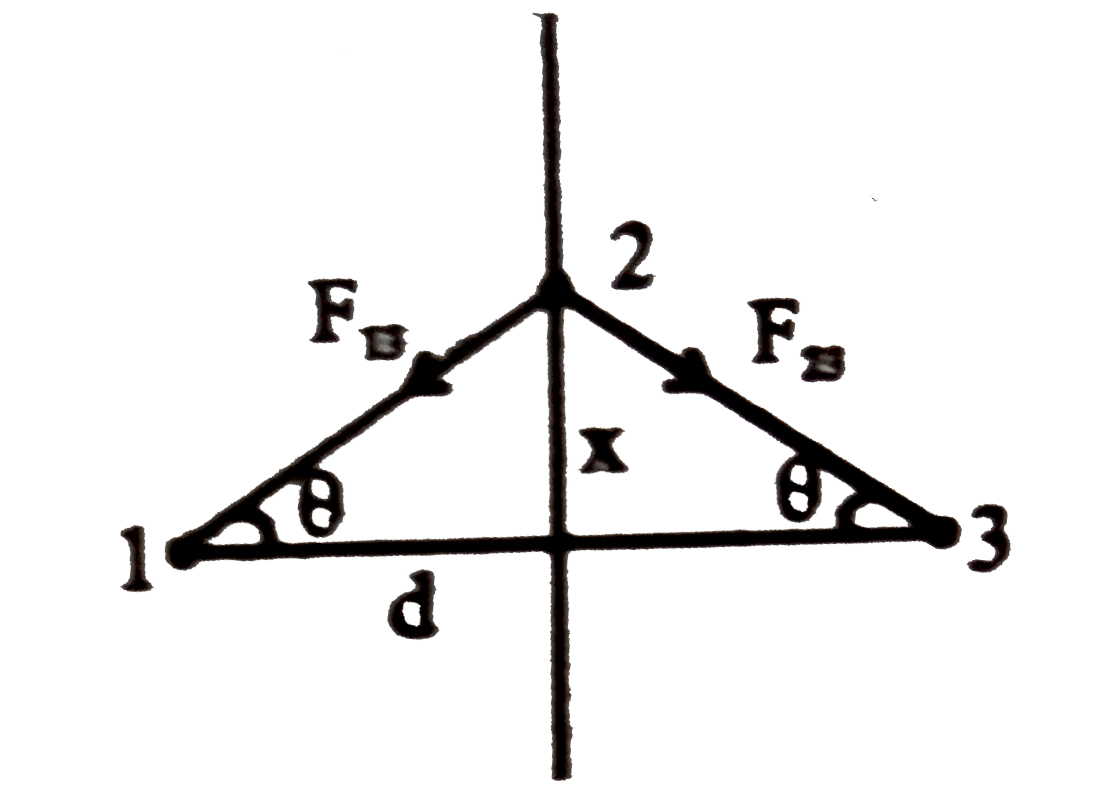
- Three infinitely long thin wires, each carrying current i in the same ...
Text Solution
|
- A long, straight wire carries a current along the z-axis. One can find...
Text Solution
|
- Three infinitely long thin wires, each carrying current i in the same ...
Text Solution
|
- Three infinitely long thein wires, each carrying curren i int eh same ...
Text Solution
|
- Two infinitely long, thin, insulated, straight wires lie in the x-y pl...
Text Solution
|
- Three infinitely long wires, each carrying a current 1A, are placed su...
Text Solution
|
- Three long wires, each carrying current i are placed as shown. The mid...
Text Solution
|
- Three infinitely long thin wires each carrying current I in the same d...
Text Solution
|
- तीन अनन्त लम्बे पतले तार, जिनमें से प्रत्येक में धारा । एक ही दिशा में...
Text Solution
|

 .
.