Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
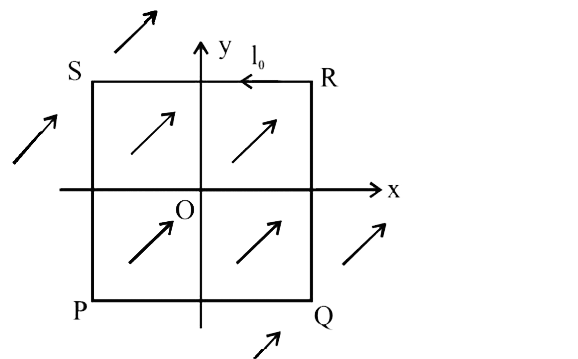
- A uniform constant magnetic field B is directed at an angle of 45^(@) ...
Text Solution
|
- A uniform constant magnetic field B is directed at an angle of 45^(@) ...
Text Solution
|
- The figure shows a wire frame in xy-plane carryigna current I . The ma...
Text Solution
|
- The rigid conducting thin wire frame carries an electric current I and...
Text Solution
|
- Current flows through uniform square frames as shown. In which case is...
Text Solution
|
- A square frame carrying a current I = 0.9 A is located in the same pla...
Text Solution
|
- A square frame carrying a current I = 0.9 A is located in the same ...
Text Solution
|
- A square frame carrying a current I is located in the same plane as a ...
Text Solution
|
- 20 सेमी भुजा का चालक-तार का एक वर्गाकार फ्रेम PQRS चित्रानुसार 0.10 टे...
Text Solution
|