A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
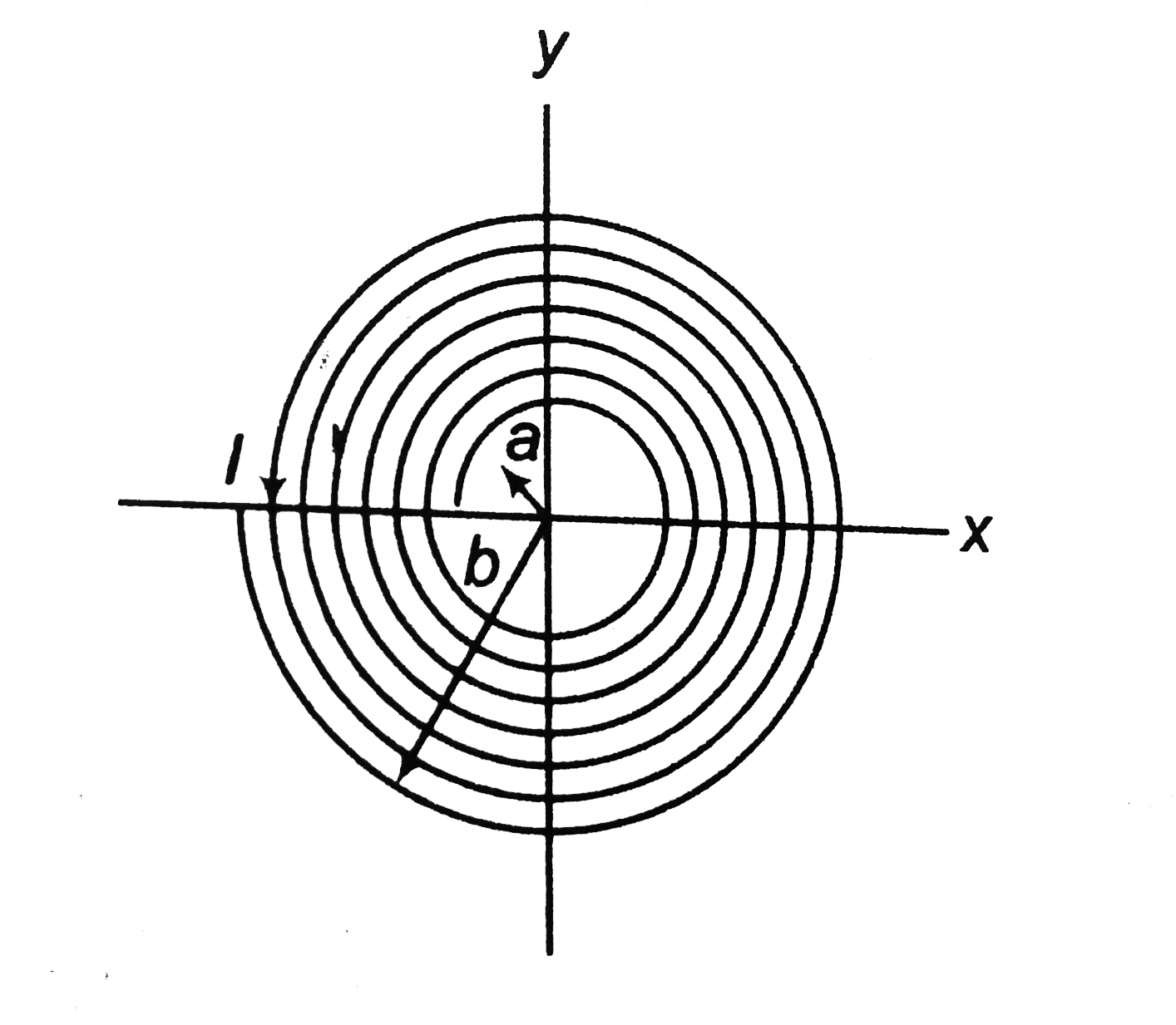
- A long insulated copper wire is closely wound as a spiral of N turns. ...
Text Solution
|
- A long insulated copper wire is closely wound as a spiral of N turns. ...
Text Solution
|
- A long insulated copper wire is closely wound as a spiral of N turns. ...
Text Solution
|
- A thin insulated wire forms a plane spiral of N=100 turns carrying a c...
Text Solution
|
- A spiral made Irorn elastic wire is connected to a DC source The spira...
Text Solution
|
- एक लम्बे वैधुत-रोधी(insulated) ताँबे के तार से N फेरों की एक कुण्डलिनी...
Text Solution
|
- A coll having N turns is wound tightly in the form of a spiral with in...
Text Solution
|
- A thin insulated wire forms a plane spiral of N = 100 tight turns carr...
Text Solution
|
- A thin insulated wire form a spiral of N= 100 turns carrying a curren...
Text Solution
|
 .
.