Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- A wheel of radius R having charg Q, uniformly distributed on the rim ...
Text Solution
|
- A string is wrapped around the rim of a wheel of moment of inertia 0.2...
Text Solution
|
- A wheel of radius R having charg Q , uniformly distributed on the rim ...
Text Solution
|
- A ring of radius R having unifromly distributed charge Q is mounted on...
Text Solution
|
- As shown in the figure, two blocks, each of mass m, suspended from the...
Text Solution
|
- a ball of mass 240g is attached to the verticle rod by means of two st...
Text Solution
|
- A mass is supported on a frictionless horizontal surface. It Is attach...
Text Solution
|
- Two blocks are attached by a light inextensible string and the system ...
Text Solution
|
- A uniform rod of mass m and length L is suspended with two massless st...
Text Solution
|
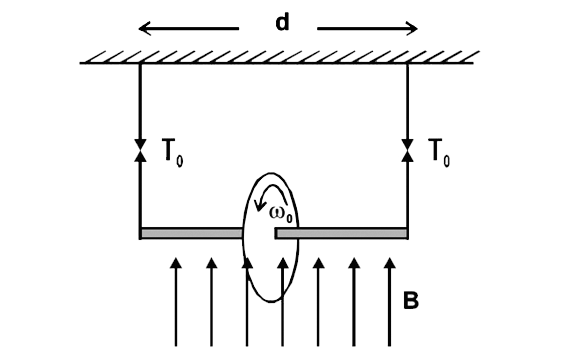
 .
.