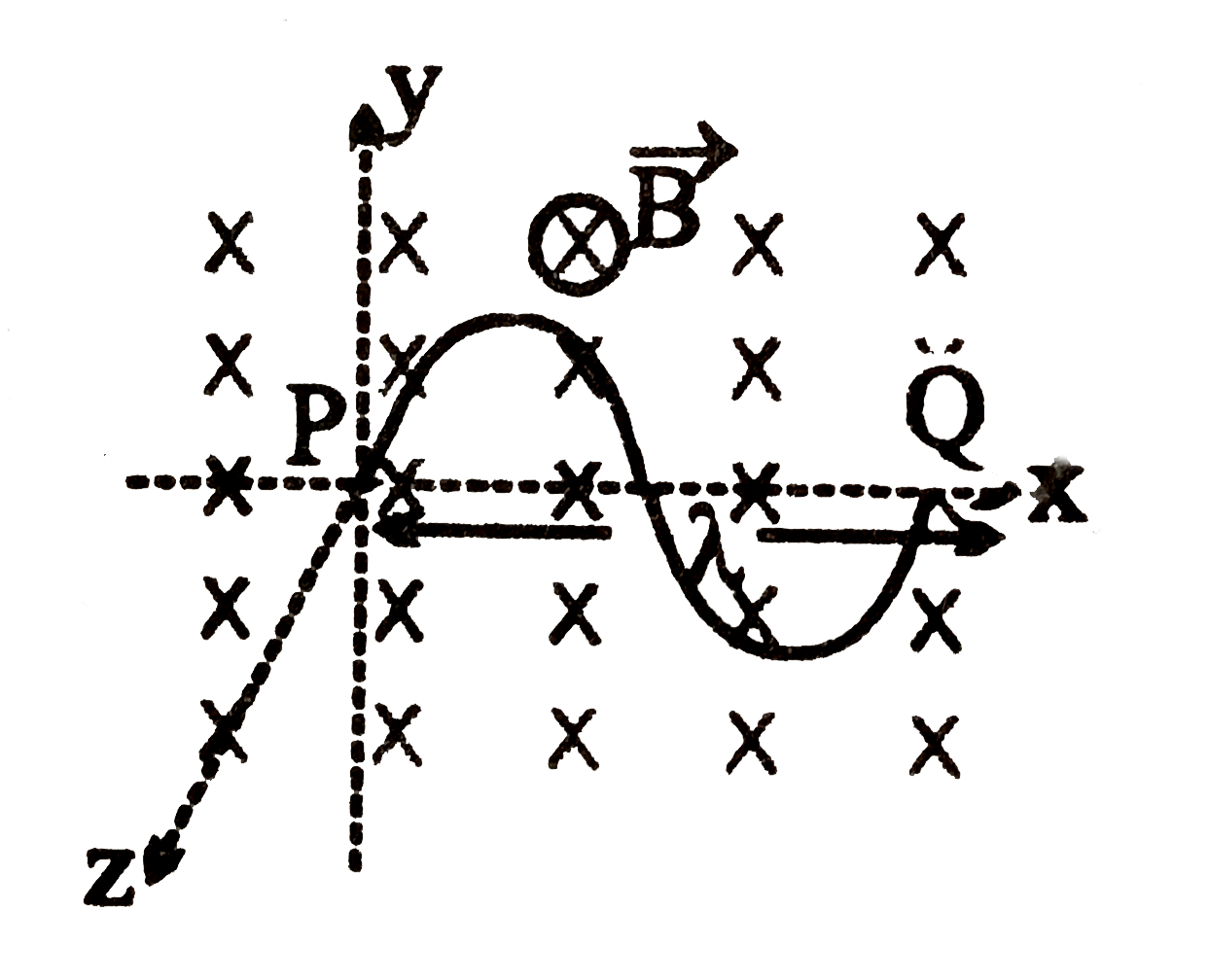Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A wire forming one cycle of sine curve is moved in x-y plane with velo...
Text Solution
|
- A portion is fired from origin with velocity vec(v) = v(0) hat(j)+ v(0...
Text Solution
|
- A wire forming one cycle of sine curve is moved in x-y plane with velo...
Text Solution
|
- A conductor AB of length l moves in x y plane with velocity vec(v) = v...
Text Solution
|
- The magnetic field in a region is given by vec(B)=B(0)(1+(x)/(a))hat(k...
Text Solution
|
- Letvec(V) =v(x)hat(i)+v(y)hat(j)+v(z)hat(k), then int(t(1))^(t(2)) V(y...
Text Solution
|
- A uniform magnetic field vec(B) = B(0) hat(k) exists in a region. A cu...
Text Solution
|
- A particle of charge q and mass m released from origin with velocity v...
Text Solution
|
- An electron is moving with an initial velocity vec(V) = v(0) hat(i) an...
Text Solution
|