Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
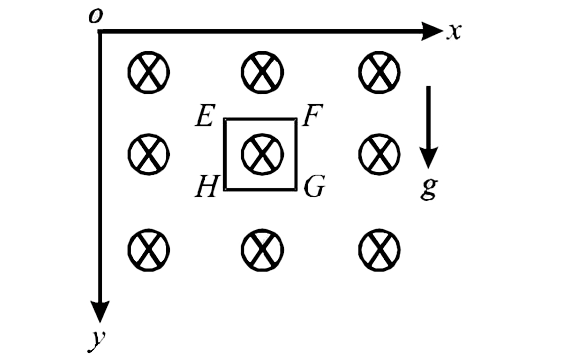
- A magnetic field B = B(0) (y//a)(hat)k is into the paper in the +z dir...
Text Solution
|
- A magnetic field B = B(0) (y//a)(hat)k is into the paper in the +z dir...
Text Solution
|
- If the work required to move the conductor shown in figure, one full t...
Text Solution
|
- The magnetic field in a region is given by vec(B)=B(0)(1+(x)/(a))hat(k...
Text Solution
|
- The magnetic field I nan reigion is given by B=B(0) (X)/(a)K. A Squrae...
Text Solution
|
- A current carrying circular loop of radius R is placed in a uniform ma...
Text Solution
|
- एक चुंबकीय क्षेत्र vec(B) = ((B(0)y)/(a))hatk कागज के तल के लंबवत अं...
Text Solution
|
- एक चुंबकीय क्षेत्र vec(B) = ((B(0)y)/(a))hatk कागज के तल के लंबवत अं...
Text Solution
|
- एक चुंबकीय क्षेत्र vec(B) = ((B(0)y)/(a))hatk कागज के तल के लंबवत अं...
Text Solution
|