Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
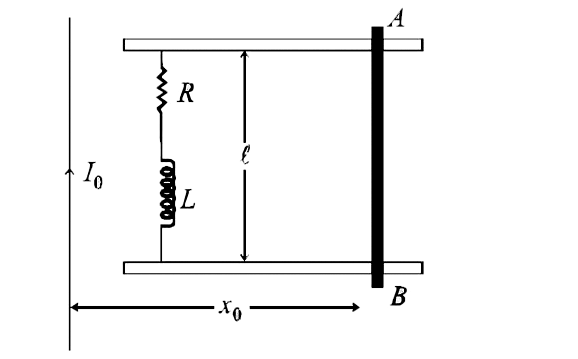
- A metal bar AB can slide on two parallel thick metallic rails separate...
Text Solution
|
- A straight wire of length l can slide on two parallel plastic rails k...
Text Solution
|
- A metal bar AB can slide on two parallel thick metallic rails separate...
Text Solution
|
- Two parallel vertical metallic rails AB and CD are separated by 1m. Th...
Text Solution
|
- A metallic rod of mass m and resistance R is sliding over the 2 conduc...
Text Solution
|
- A metallic rod of mass m and resistance R is sliding over the 2 conduc...
Text Solution
|
- Figure shows a wire sliding on two parallel, conducting rails placed a...
Text Solution
|
- Two long fixed parallel vertical conducting rails AB and CD are separa...
Text Solution
|
- Figure shows a wire of resistance R sliding on two parallel, conductin...
Text Solution
|