Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A long solenoid of radius a and number of turns per unit length n is e...
Text Solution
|
- The current in a long solenoid of radius R and having n turns per unit...
Text Solution
|
- A long solenoid of radius a and number of turns per unit length n is e...
Text Solution
|
- A very long straight solenoid has a cross section radius R. A numbe...
Text Solution
|
- A long straight solenoid has n turns per unit length. An alternating c...
Text Solution
|
- An infinite long straight conducting cylinderical shell of radius a is...
Text Solution
|
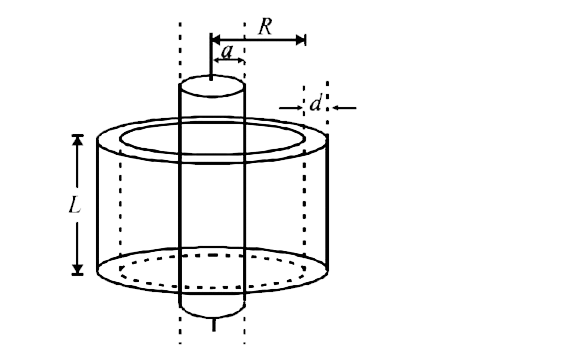
- A solenoid of radius R number of turn per unit length n and length L h...
Text Solution
|
- A conducting ring of radius b is placed coaxially in a long solenoid o...
Text Solution
|
- एक a त्रिज्या तथा प्रति एकांक लम्बाई में । फेरों वाली लम्बी परिनालिका ...
Text Solution
|