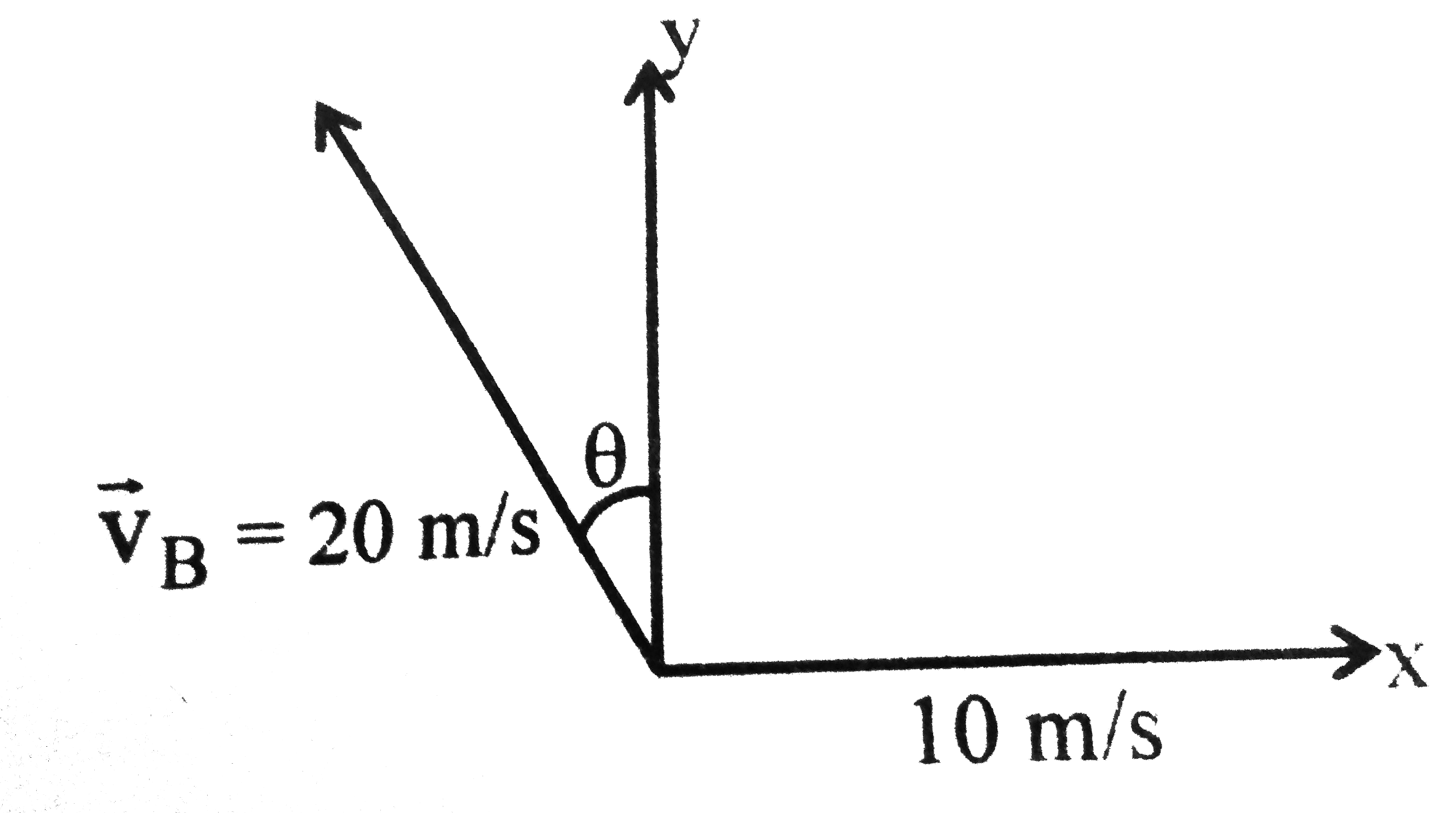
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two boats A and b move away form a buoy anchored at the middle of a ri...
Text Solution
|
- The current velocity of river grows in proportion to the distance from...
Text Solution
|
- A river of width omega is flowing with a uniform velocity v. A boat st...
Text Solution
|
- Two boats A and B moved away from a buoy anchored in the middle of a r...
Text Solution
|
- Two boats A and B having same speed relative to river are moving in a ...
Text Solution
|
- Two boats A and b move away form a buoy anchored at the middle of a ri...
Text Solution
|
- Two boats, A and B, move away from a buoy anchored at the middle of a ...
Text Solution
|
- Two boats, A and B , move away from a point P at the middle of a river...
Text Solution
|
- Twp boats are moving along perpendicular paths on a still take at righ...
Text Solution
|