Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
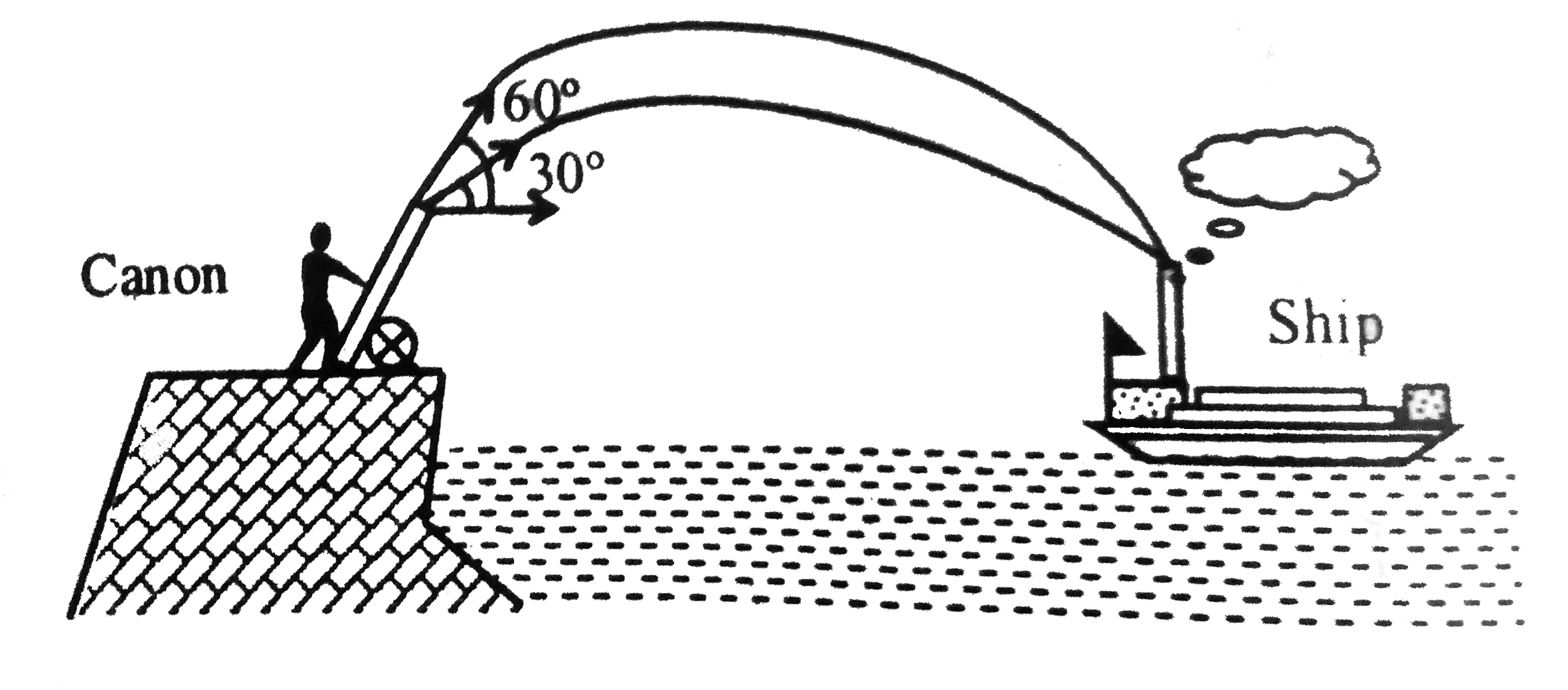
- At aharbour enemy ship is at a distance 180sqrt(3)m form the security ...
Text Solution
|
- A ship sends out ultrasound that returns form the seabed and is detect...
Text Solution
|
- At aharbour enemy ship is at a distance 180sqrt(3)m form the security ...
Text Solution
|
- एक टॉप, जो 60 मीटर/स्कन्द के वेग से गोला फेकती है, से शत्रु का जहाज 18...
Text Solution
|
- एक जहाज 60 किमी/घण्टा के क्षैतिज वेग से पृथ्वी तल से 490 मीटर की ऊँचाई...
Text Solution
|
- In in ocean surveillance system of ship fitted with a (RADAR) the time...
Text Solution
|
- Two ships are sailing in the sea on the two side of lighthouse of heig...
Text Solution
|
- A ship is moving towards east at 10km*h^(-1). A boat is moving north ...
Text Solution
|
- धरती पर A से एक विमान का उन्नयन कोण 45^@ है । 15 सेंकड की उड़ान के पश्...
Text Solution
|