A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
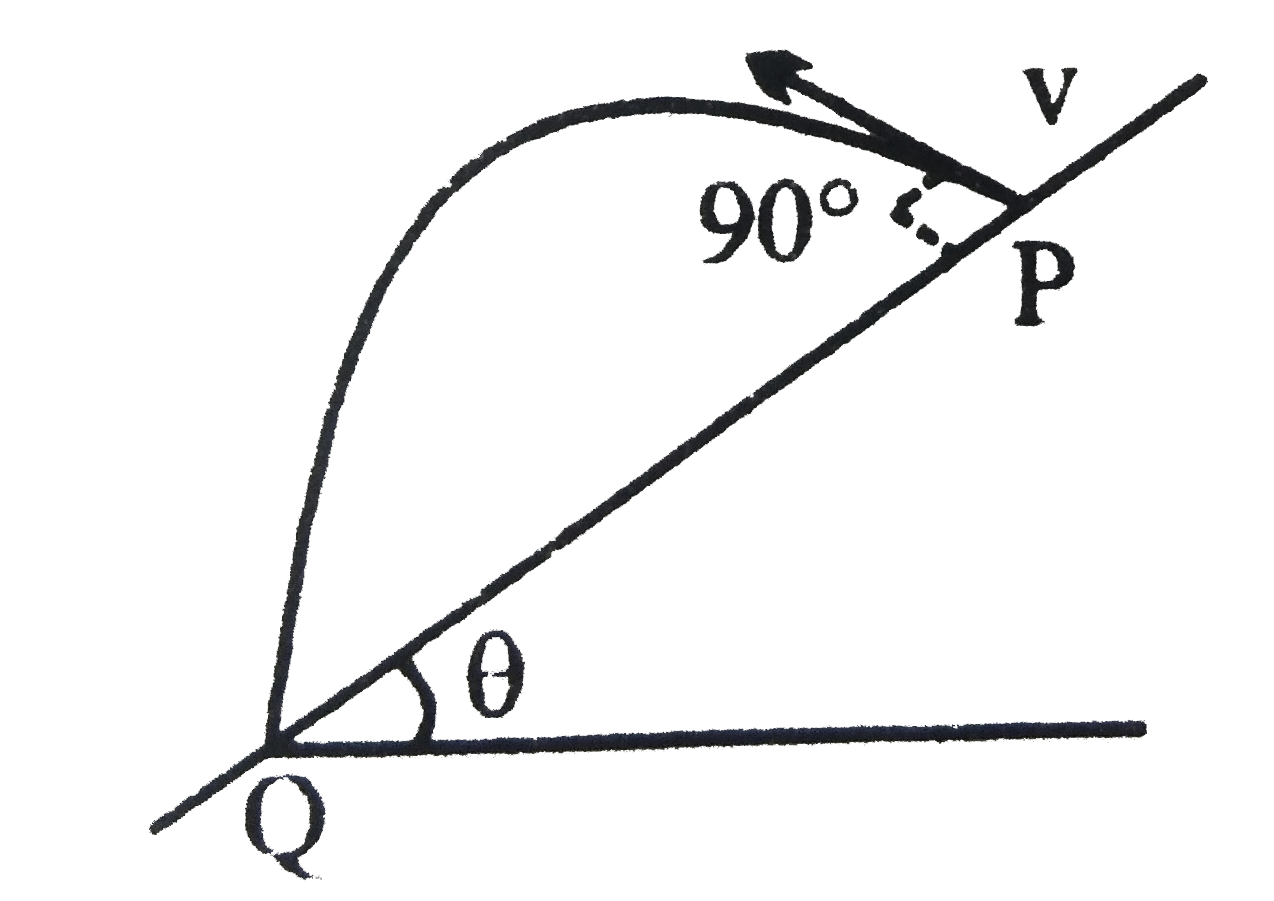
- If time taken by the projectile to reach Q is T, than PQ =
Text Solution
|
- In the time taken by the projectile to reach from A to B is t . Then t...
Text Solution
|
- A projectile is thrown at angle beta with vertical.It reaches a maximu...
Text Solution
|
- Time taken by the particle to reach from A to B is t . Then the distan...
Text Solution
|
- A projectile is thrown at angel with vertical. It reaches a maximum he...
Text Solution
|
- In figure shown below, the time taken by the projectile to reach from ...
Text Solution
|
- A ball dropped from a point P crosses a point Q in t seconds. The time...
Text Solution
|
- Two projectiles are thrown with different velocities and at different ...
Text Solution
|
- A ball dropped from a point P crosses a point Q in t seconds. The time...
Text Solution
|