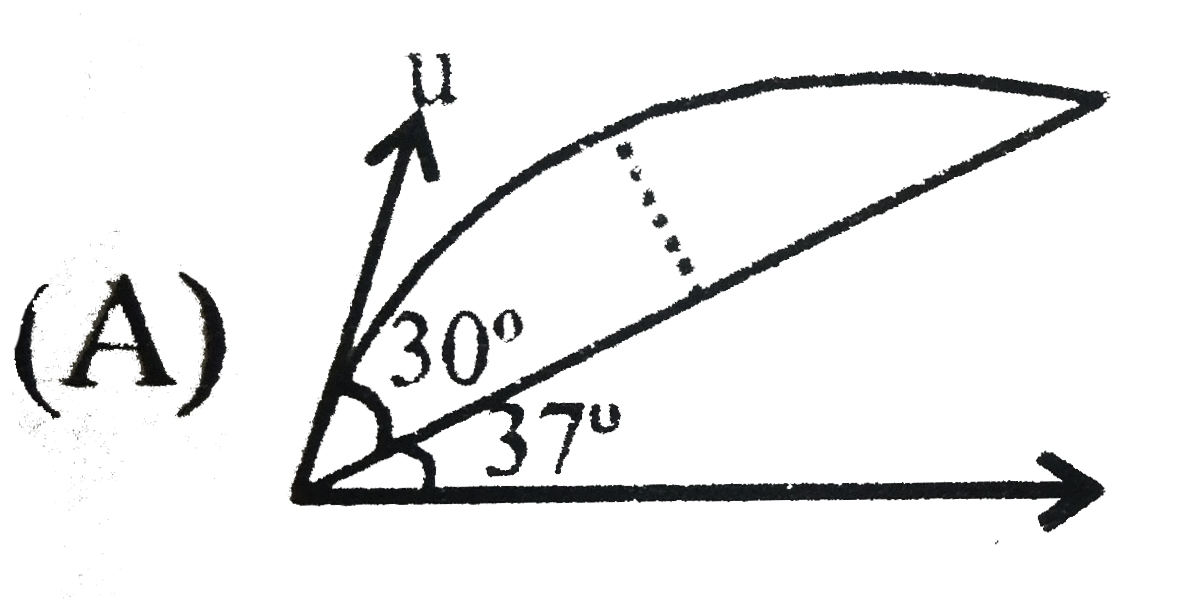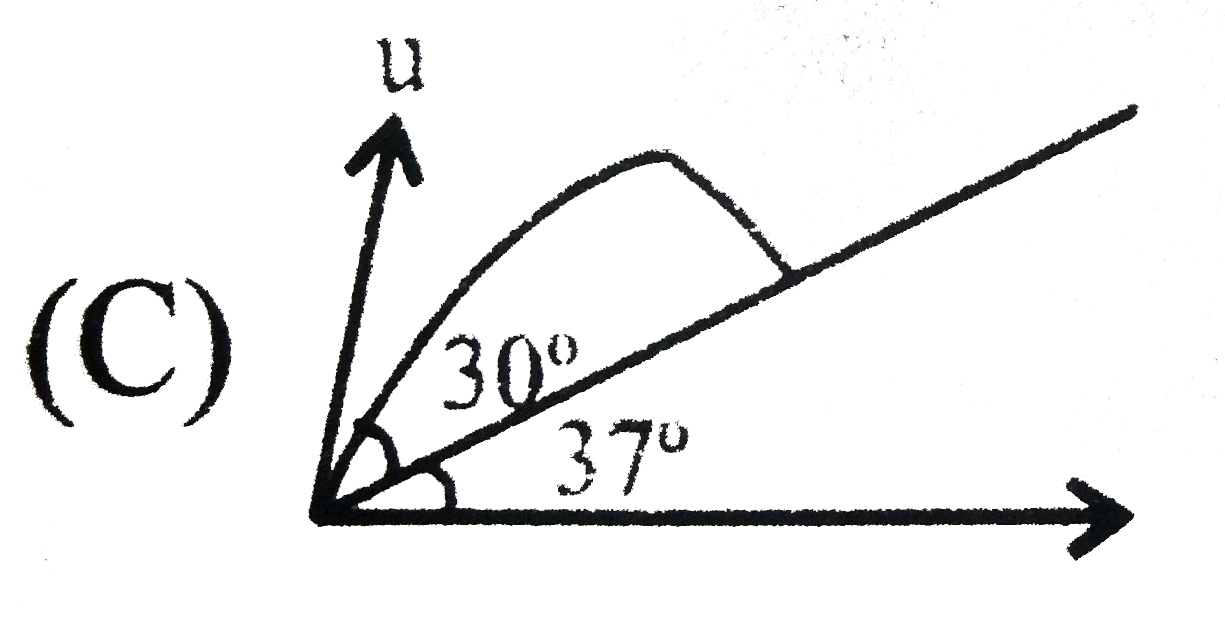A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle is projected with velocity 30^(@) above on an inclined plan...
Text Solution
|
- A particle is projected from the bottom of an inclined plane of inclin...
Text Solution
|
- A particle is projected with a certain velocity at an angle prop above...
Text Solution
|
- In figure, the angle of inclination of the inclined plane is 30^@ . Fi...
Text Solution
|
- A particle is projected from the inclined plane at angle 37^(@) with t...
Text Solution
|
- A particle is projected with velocity 30^(@) above on an inclined plan...
Text Solution
|
- A particle is projected with a certain velocity at an angle alpha abov...
Text Solution
|
- A particle is projected with a velocity of 20 m/s at an angle of 30^(@...
Text Solution
|
- A particle projected horizontally from the top of an inclined plane in...
Text Solution
|