Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
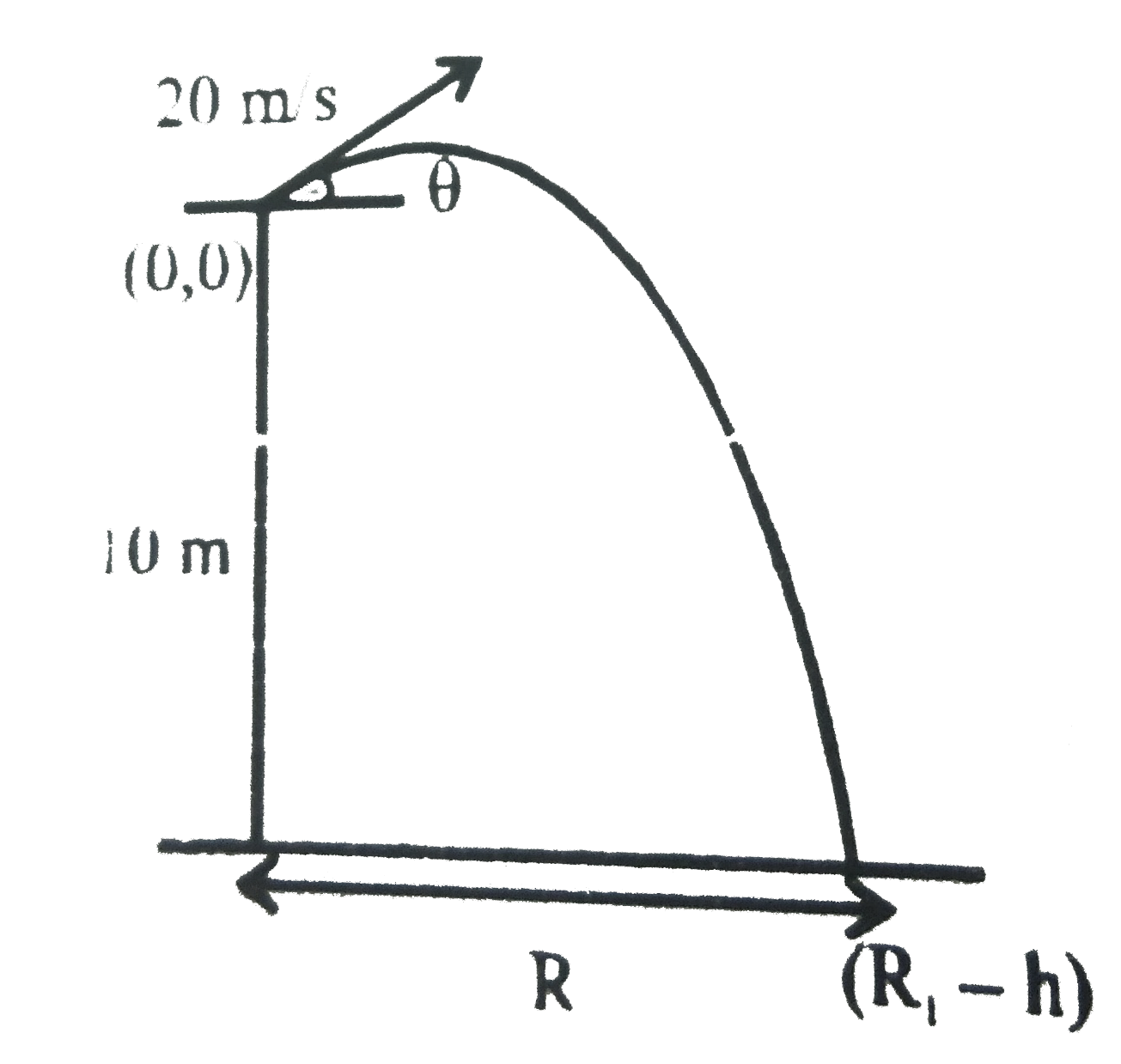
- A parojectile thrown from platform at a height 10 m above the gorund w...
Text Solution
|
- A parojectile thrown from platform at a height 10 m above the gorund w...
Text Solution
|
- A projectile thrown from a height of 10 m with velocity of sqrt(2)m//s...
Text Solution
|
- A ball is thrown from the top of a tower with an initial velocity of 1...
Text Solution
|
- A projectile is thrown at angle of 30^(@) with a velocity of 10m/s .Th...
Text Solution
|
- The equation of trajectory of a projectile thrown from a point on the ...
Text Solution
|
- A projectile is thrown at an angle of 30^(@) with a velocity of 10m/s....
Text Solution
|
- A projectile is thrown at an angle of 30^@ with a velocity of 10m/s. t...
Text Solution
|
- A projectile is thrown at an angle of 30^@ with a velocity of 10m/s. t...
Text Solution
|