Home
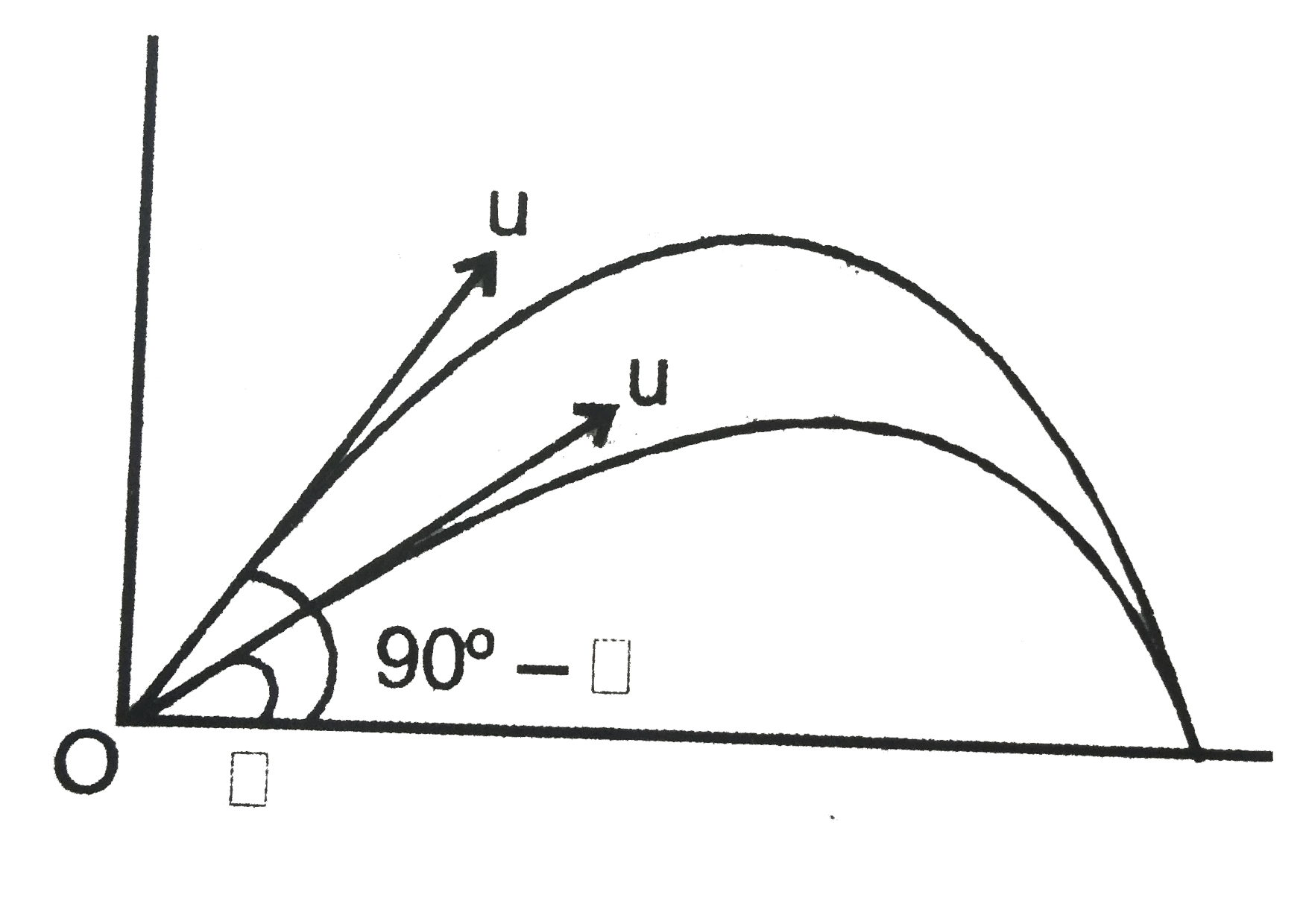
Class 11
PHYSICS
A projectile can have same range R for t...

A projectile can have same range `R` for two angles of projection. It `t_1 and t_2` are the times of flight in the two cases, then what is the product of two times of flight ?

A

`t_(1)t_(2) prop R^(2)`

B

`t_(1)t_(2) prop R`

C

`t_(1)t_(2) prop (1)/(R )`

D

`t_(1)t_(2) prop (1)/(R^(2))`

Text Solution

Verified by Experts

The correct Answer is:
B
A projectile can have same range if angles of projection are complementary i.e. `theta` and `(90^(@) - theta)`. Thus, in both cases:
`t_(1) = (2u sin theta)/(g)`
`t_(2) 2usin (90^(@) - theta)/(g)`
`= (2u cos theta)/(g)`
From eq. (i) and (ii)
`t_(1)t_(2) = (4u sin theta cos theta)/(g^(2))`
`= (2u^(2)sin 2theta)/(g^(2))`
`:. t_(1)t_(2) = (2R)/(g) (therefore R = (u^(2)sin 2 theta)/(g))`
Hence, `t_(1)t_(2) prop R`
Promotional Banner

Similar Questions

Explore conceptually related problems

A projectile can have the same range R for two angles of projection. If t_(1) and t_(2) be the times of flight in the two cases:-

A projectile can have the same range R for two angles of projection .If t_1 and t_2 be the times of flight in the two cases, then the product of the two times of fight is directly proportional to

A projectile can have the same range 'R' for two angles of projection . If 'T_(1)' and 'T_(2)' to be times of flights in the two cases, then the product of the two times of flights is directly proportional to .

A projectile can have the same range R for two angle of projection . If t-1 and t_2 be the terms of flight in the two cased then the initial velocity of projectile is?

A projectille can have the same range R for two angles of projection. If t_(1) and t_(2) be the time of flight in the two cases, then find the relation between t_(1), t_(2) and R .

For a given velocity, a projectile has the same range R for two angles of projection. If t_(1) and t_(2) are the time of flight in the two cases, then t_(1) = t_(2) is equal to

For a given velocity, a projectile has the same range R for two angles of rpojection if t_(1) and t_(2) are the times of flight in the two cases then

A projectile has the same range R for two angles of projections but same speed. If T_(1) and T_(2) be the times of flight in the two cases, then Here theta is the angle of projection corresponding to T_(1) .

A projectile has the same range R for angles of projections. If T_(1) and T_(2) be the times of fight in the two cases, then ( using theta as the angle of projection corresponding to T_(1) )