Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
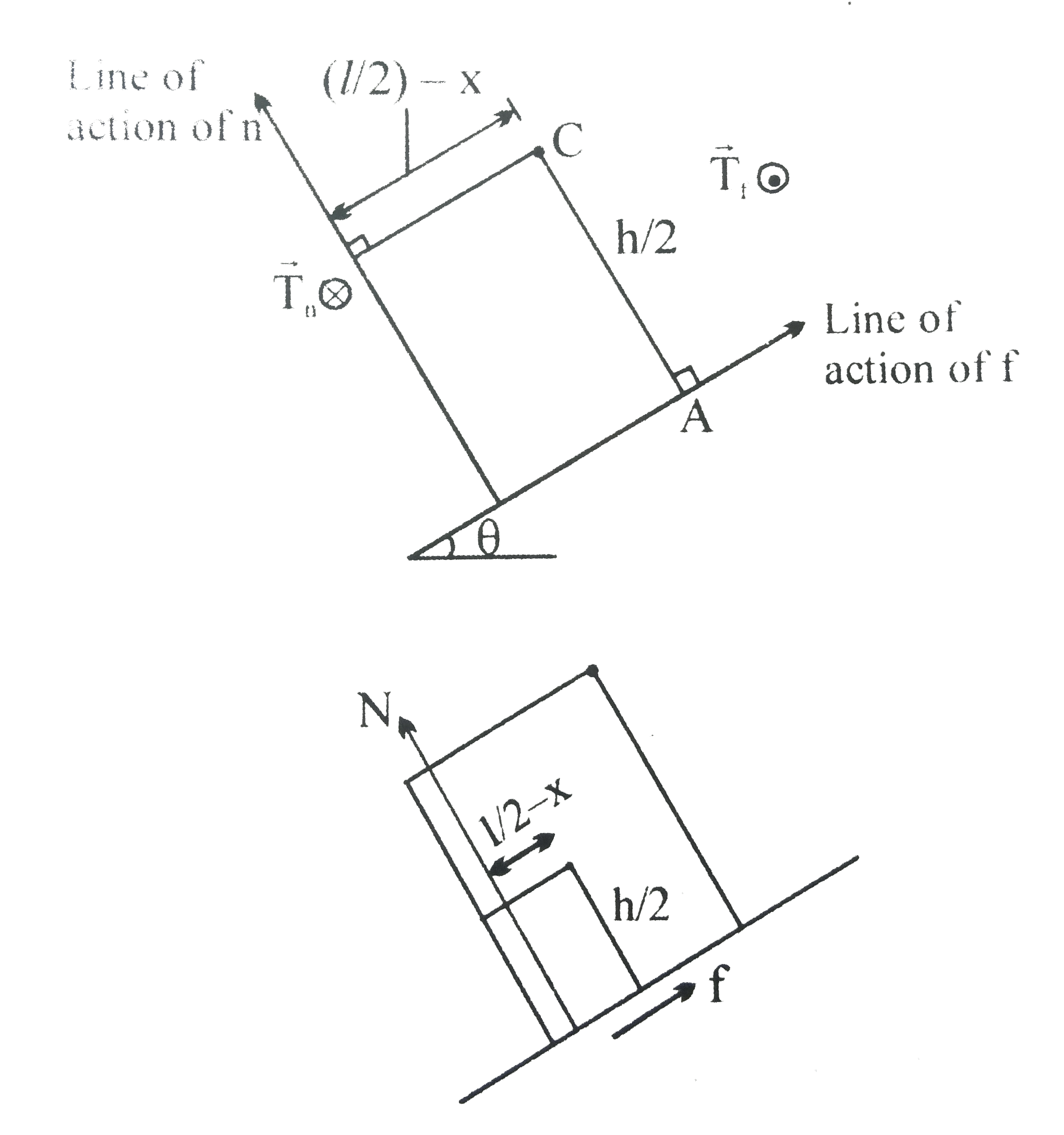
- The centre in figure has dimensions m by h and the ramp is inclined a...
Text Solution
|
- A block of mass m is placed on a smooth inclined plane of inclination ...
Text Solution
|
- A cubical block of mass M and edge a slides down a rougg inclined plan...
Text Solution
|
- A heavy block of length b and height h is placed at rest on a rough in...
Text Solution
|
- A horizontal force acting on a block of mass m which is placed on an i...
Text Solution
|
- The centre in figure has dimensions m by h and the ramp is inclined a...
Text Solution
|
- The figure shows a horizontal force vecF acting on a block of mass M o...
Text Solution
|
- The crate in Fig. 11-20 has dimensions I by h and the ramp is inclined...
Text Solution
|
- In Fig. 5-45, a crate of mass m = 115 kg is pushed at constant speed u...
Text Solution
|