Home
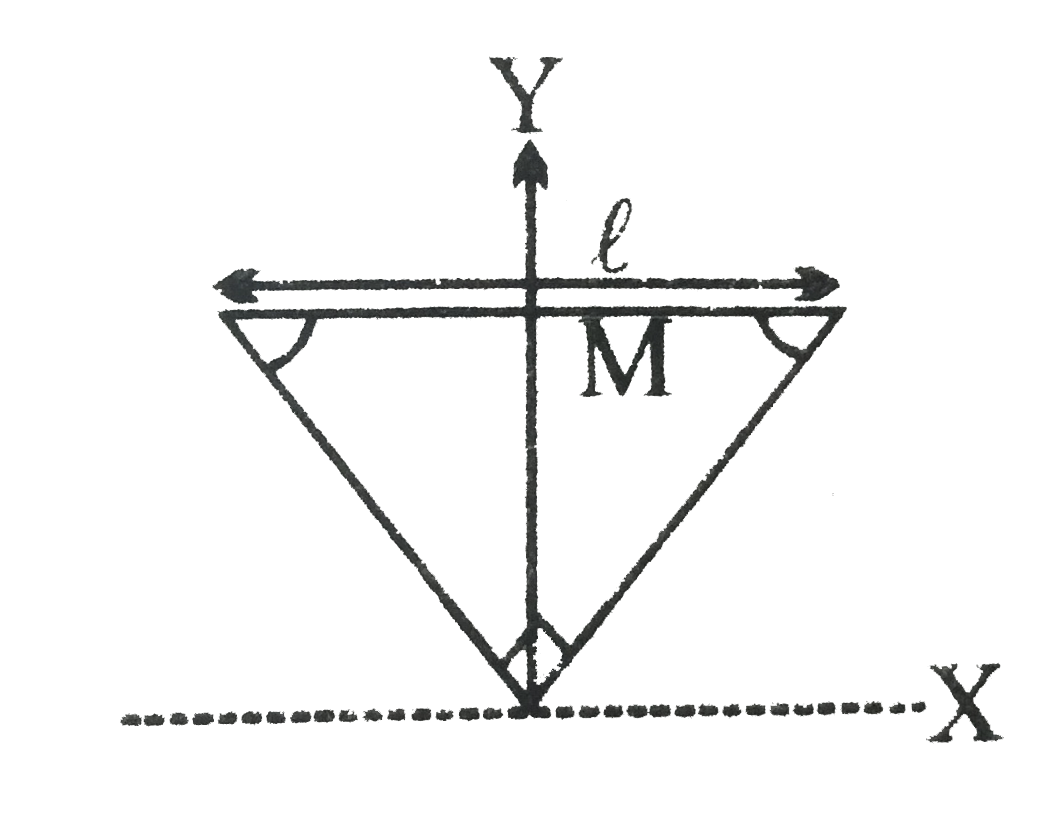
Class 11
PHYSICS
The figure shows an isosceles triangle p...

The figure shows an isosceles triangle plate of mass `M` and base `L`.
The angle at the apex is `90^@`. The apex lies at the origin and the base is parallel to `X-`axis.

The moment of inertia of the plate about the `z-`axis is

A

`(ML^(2))/(6)`

B

`(ML^(2))/(8)`

C

`(ML^(2))/(24)`

D

none of these

Text Solution

Verified by Experts

The correct Answer is:
C
From `_|_` axis theorem
`I_(z) = I_(x) + I_(y)`
`I_(y) = I_(z) - I_(x) = (mL^(2))/(6) - (mL^(2))/(8) rArr I_(y) = (mL^(2))/(24)`.
Promotional Banner

Similar Questions

Explore conceptually related problems

The figure shows an isosceles triangle plate of mass M and base L . The angle at the apex is 90^@ . The apex lies at the origin and the base is parallel to X- axis. The moment of inertia of the plate about its base parallel to the x- axis is

The figure shows an isosceles triangular plate of mass M and base L. The angle at the apex is 90^(@) . The apex lies at the origin and the base is parallel to X - axis. The moment of inertia of the plate about its base parallel to the x-axis is

A wire of mass m and length l is bent in the form of circular ring. The moment of inertia of the ring about its axis is

A uniform rectangular plate has side length l and 2 l . The plate is in x - y plane with its centre at origin and sides parallel to x and y axes. The moment of inertia of the plate about an axis passing through a vertex (say A) perpendicular to the plane of the figure is I_(0) . Now the axis is shifted parallel to itself so that moment of inertia about it still remains I_(0) . Write the locus of point of intersection of the axis with xy plane

A thin wire of mass M and length L is turned into a ring. The moment of inertia about its axis will be:

Let I be the moment of interia of a uniform square plate about an axis AB that passses through its centre and is parallel to two its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle theta with AB . The moment of inertia of the plate about the axis CD is then equal to-

A moment of inertia of a thin circular plate is minimum about the following axis