A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
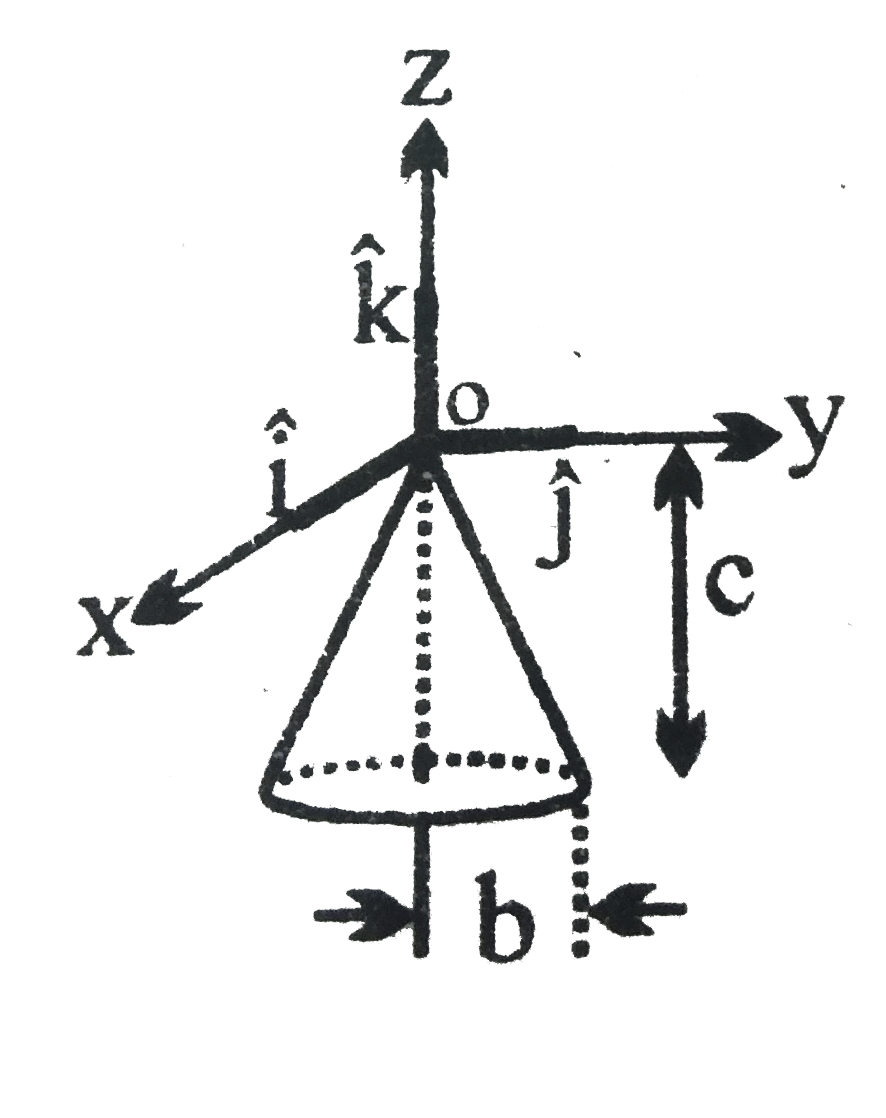
- A solid cone hanges from a frictionless pivot at the origin O, as show...
Text Solution
|
- The force 7 hat i+ 3 hat j - 5 hat k acts on a particle whose position...
Text Solution
|
- A solid cone hanges from a frictionless pivot at the origin O , as sho...
Text Solution
|
- the unit vector hat(i),hat(j) and hat(k) are as shown below. What will...
Text Solution
|
- The torque of force F = -3 hat(i)+hat(j) + 5 hat(k) acting on a point ...
Text Solution
|
- Find the torque of a force 7 hat(i) + 3 hat(j) - 5 hat(k) about the or...
Text Solution
|
- The torque of force barF= (2 hat i -3 hat j + 4 hat k) newton acting a...
Text Solution
|
- A force vec(F) = (2 hat(i) + 3 hat(j) + 4 hat(k)) N is applied to a po...
Text Solution
|
- मूल बिंदु के परित 7 hat(i) + 3 hat(j) - 5 hat(k) का बल आघूर्ण ज्ञात की...
Text Solution
|
 .
.