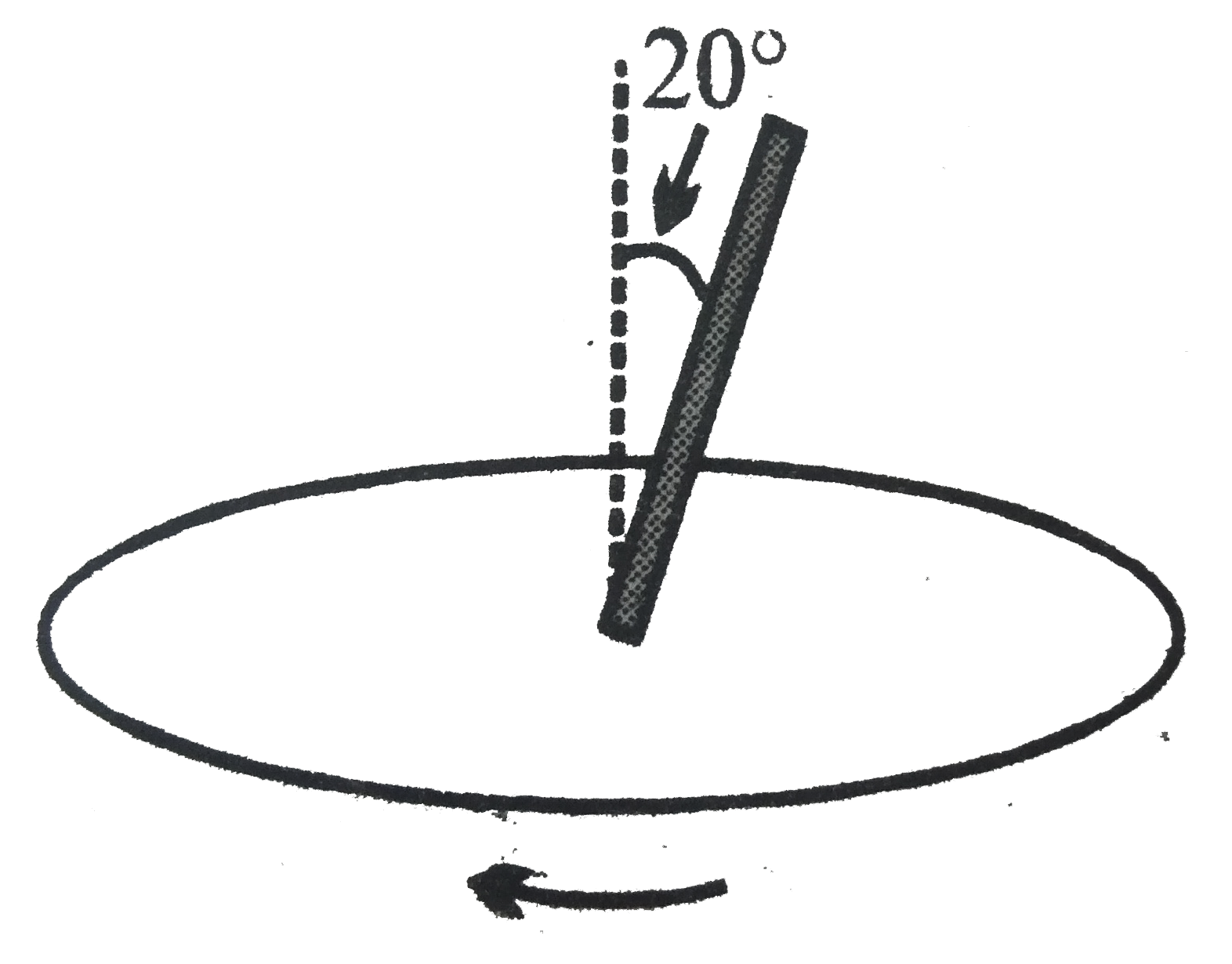
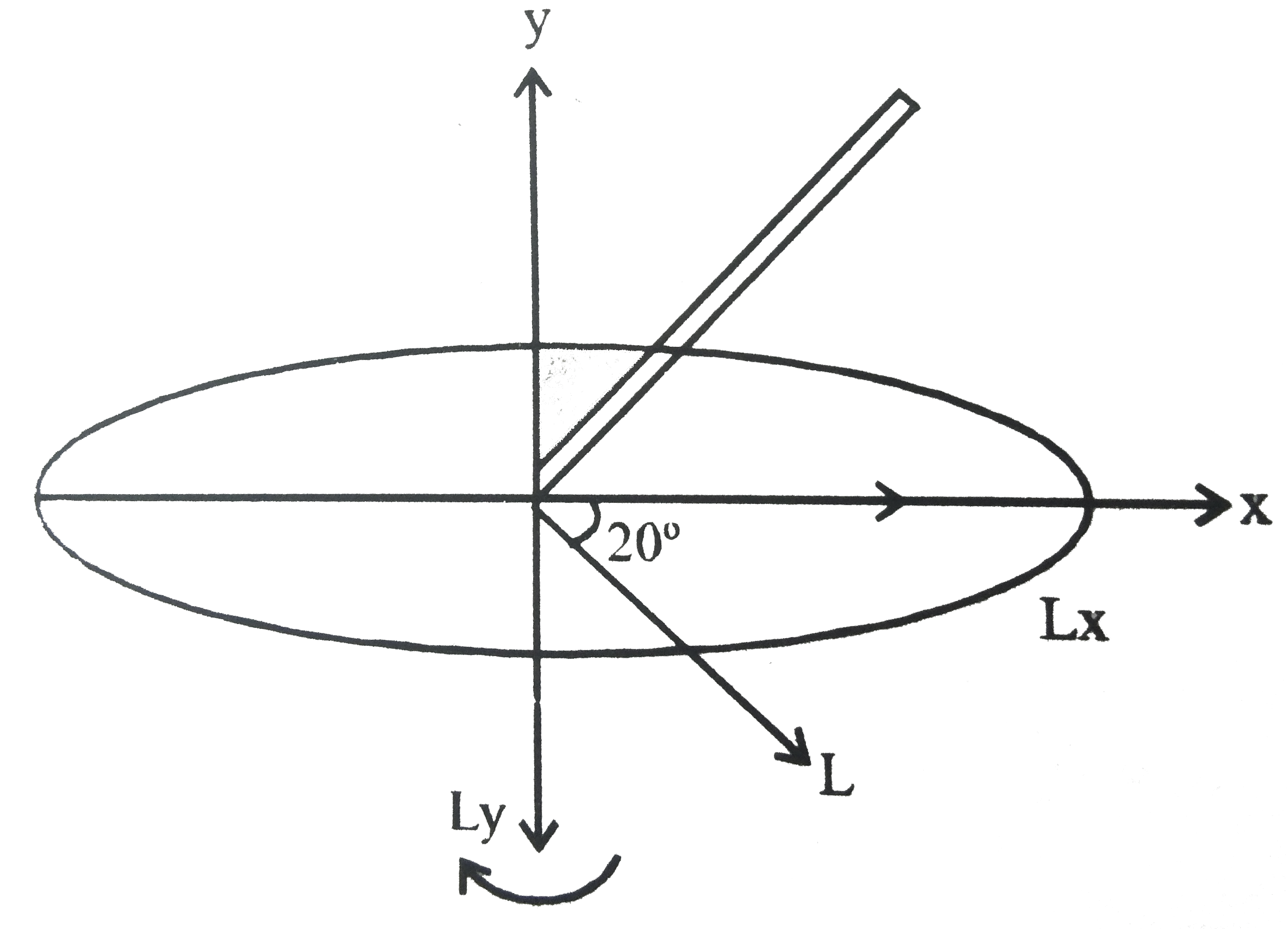
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A uniform rod is fixed to a rotating turntable so that its lower end i...
Text Solution
|
- A uniform rod of mass m and length l rotates in a horizontal plane wit...
Text Solution
|
- A uniform rod of mass m and length l(0) is rotating with a constant an...
Text Solution
|
- A uniform rod is fixed to a rotating turntable so that its lower end i...
Text Solution
|
- A uniform rod is fixed to a rotating turntable so that its lower end i...
Text Solution
|
- A conical pendulum, a thin uniform rod of length l and mass m , rotate...
Text Solution
|
- A thin uniform copper rod of length l and mass m rotates uniformly wit...
Text Solution
|
- A uniform metal rod is rotated in horizontal plane about a vertical ax...
Text Solution
|
- A uniform rod AB of mass m and length L rotates about a fixed vertical...
Text Solution
|
 .
.  .
.