A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A hollow smooth uniform A of mass 'm' rolls without sliding on a smoot...
Text Solution
|
- A sphere of mass m and radius R rolls without sliding on a horizontal ...
Text Solution
|
- A solid sphere rolls on a smooth horizontal surface at 10 m//s and the...
Text Solution
|
- A particle of mass m moving with velocity v(0) collides with sphere of...
Text Solution
|
- A small ball ( uniform solid sphere ) of mass m is released from the t...
Text Solution
|
- A sphere of radius R and mass M collides elastically with a cubical bl...
Text Solution
|
- A smooth sphere A of mass 0.1kg is moving with speed 5m//s when it col...
Text Solution
|
- A loop of mass M and radius R is rolling on a smooth horizontal surfac...
Text Solution
|
- A solid cylinder of mass 1 kg and radius 0.02 m, is rolling on a smoot...
Text Solution
|
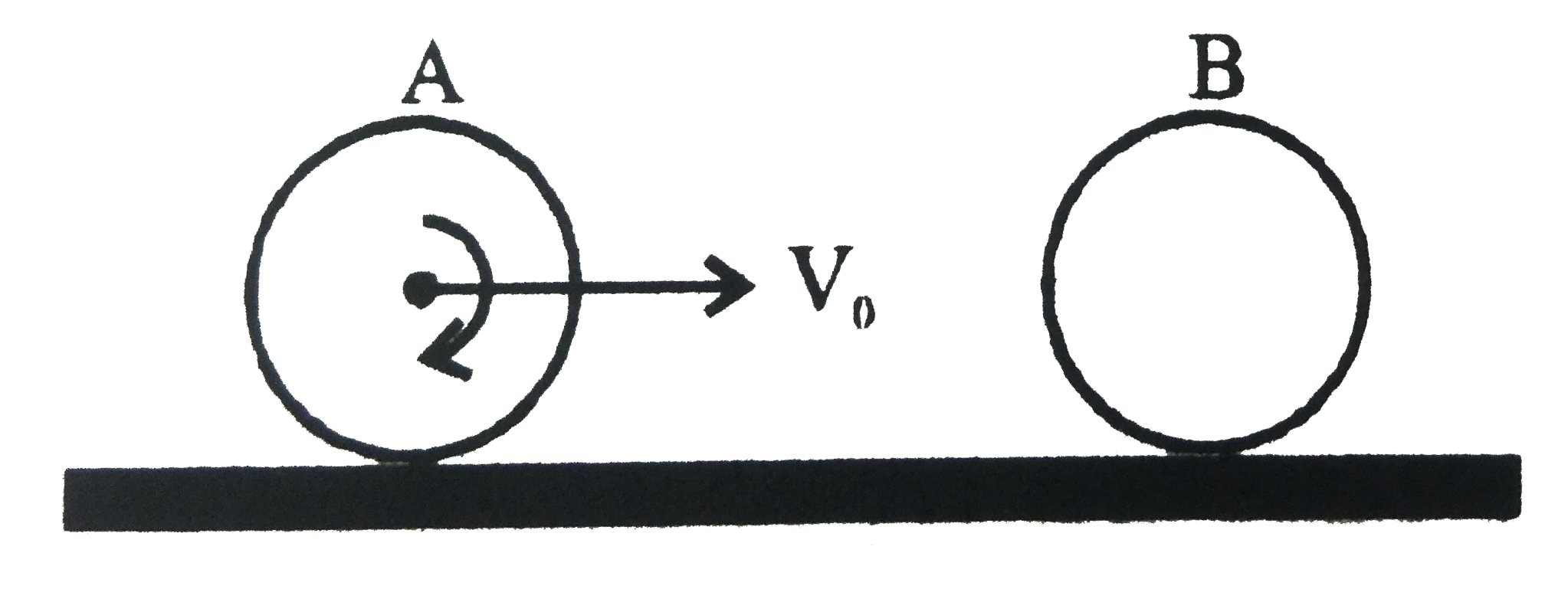 .
.