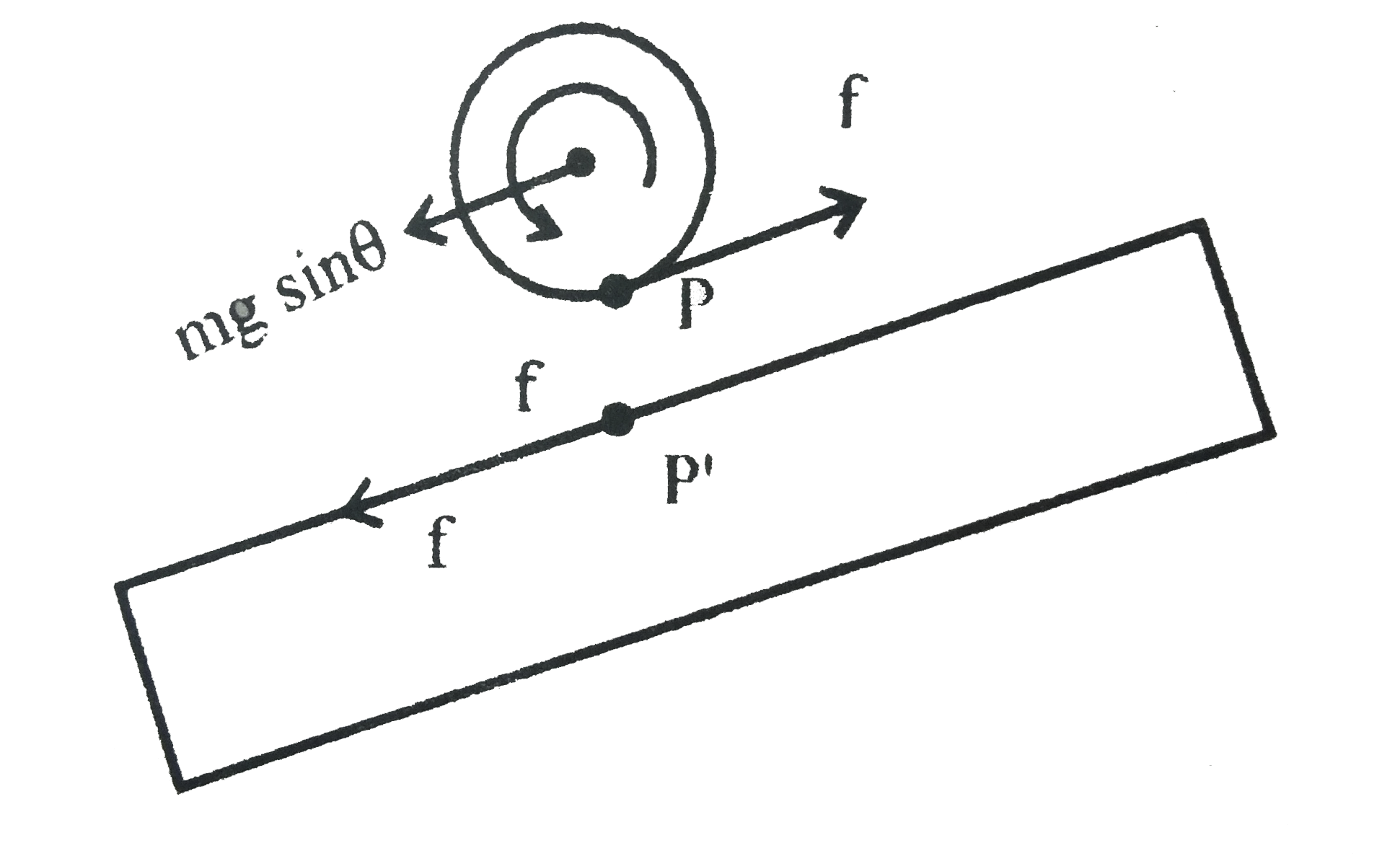
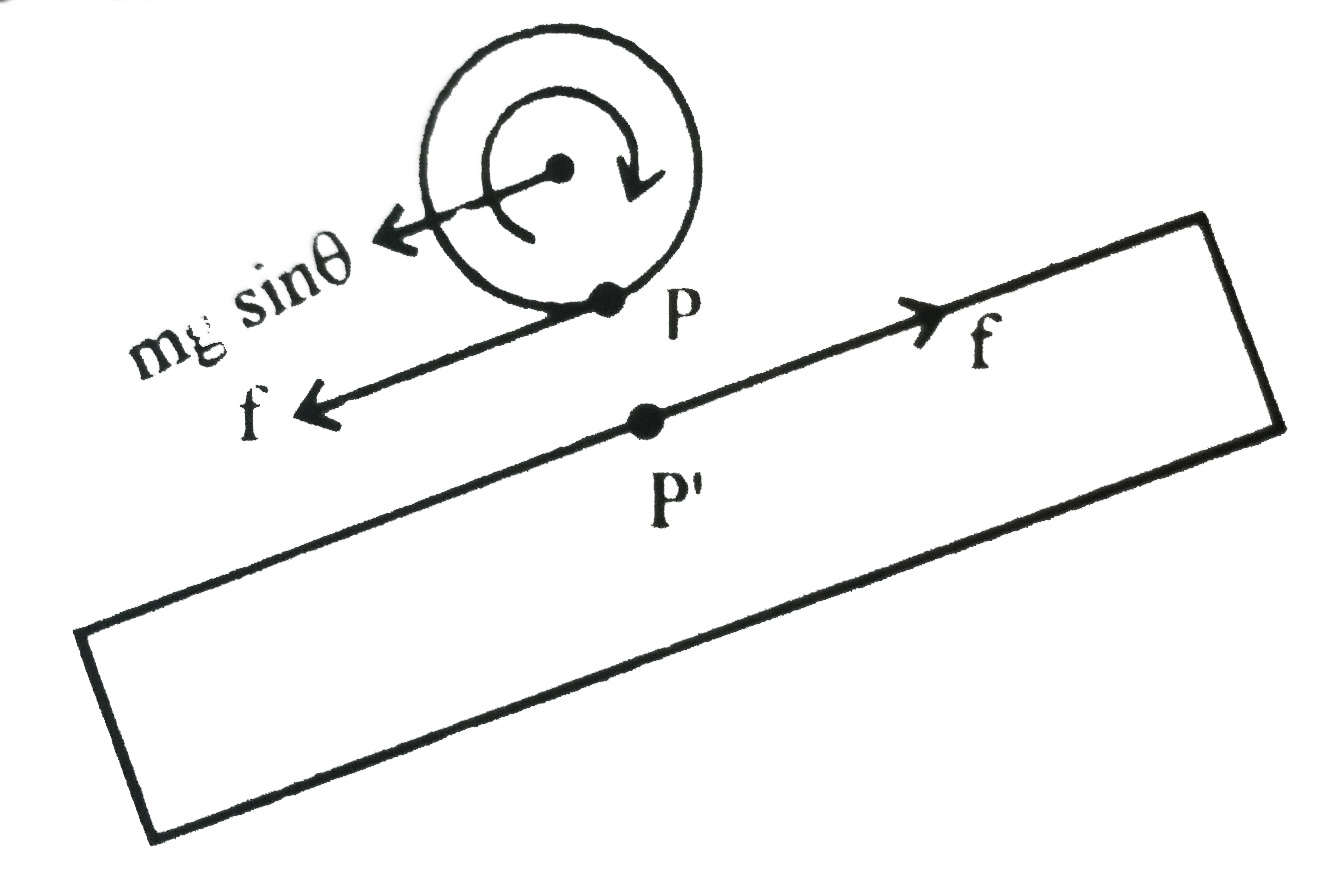
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A plank of mass M is placed over smooth inclined plane and sphere is a...
Text Solution
|
- A sphere of mass m and radius r is placed on a rough plank of mass M ....
Text Solution
|
- A plank with a uniform sphere placed on it resting on a smooth horizon...
Text Solution
|
- A plank with a uniform sphere placed on it rests on a smooth horizonta...
Text Solution
|
- A plank of mass M is placed over smooth inclined plane and sphere is a...
Text Solution
|
- A plank with a uniform sphere placed on it. Rests on a smooth horizont...
Text Solution
|
- Consider the system shown. A solide sphere (of mass m and radius R) is...
Text Solution
|
- Consider the system shown. A solide sphere (of mass m and radius R) is...
Text Solution
|
- A solid sphere of mass m and radius R is placed over a plank of same m...
Text Solution
|
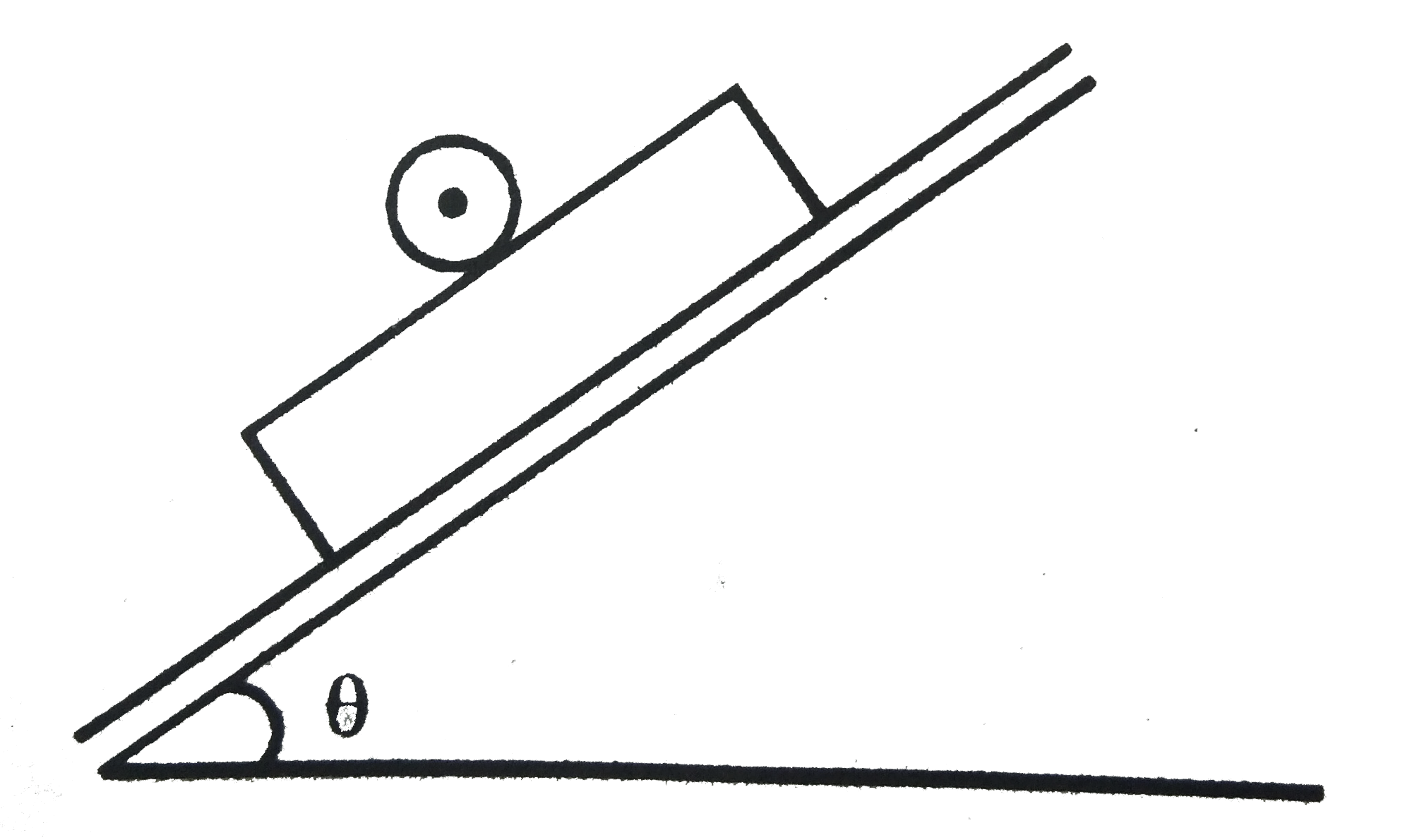 .
.