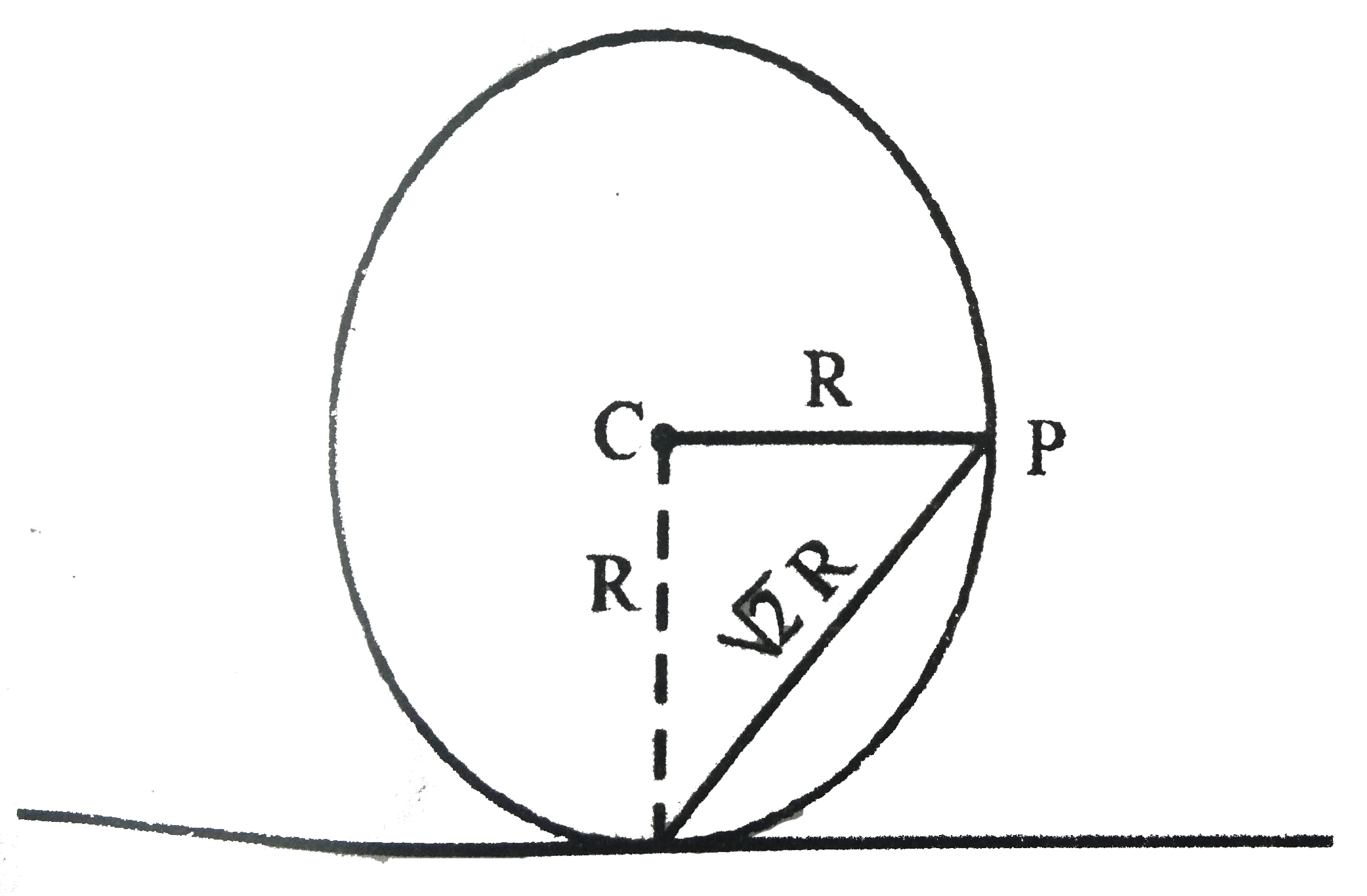A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A ring rolls without slipping on the ground. Its centre C moves with a...
Text Solution
|
- A hoop rolls on a horizontal ground without slipping with linear speed...
Text Solution
|
- Three indential rings move with same speed on a horizontal magnetic fi...
Text Solution
|
- A ring rolls without slipping on the ground. Its centre C moves with a...
Text Solution
|
- A wheel of radius R=0.1m is rolling without slipping on a horizontal s...
Text Solution
|
- A uniform ring rolls on a horizontal surface with out slipping. Its ce...
Text Solution
|
- In pure rolling motion of a ring (a) it rotates about instantaneous po...
Text Solution
|
- In pure rolling motion of a ring (a) it rotates about instantaneous ...
Text Solution
|
- Two identical rings are moving with equal kinetic energy One ring roll...
Text Solution
|

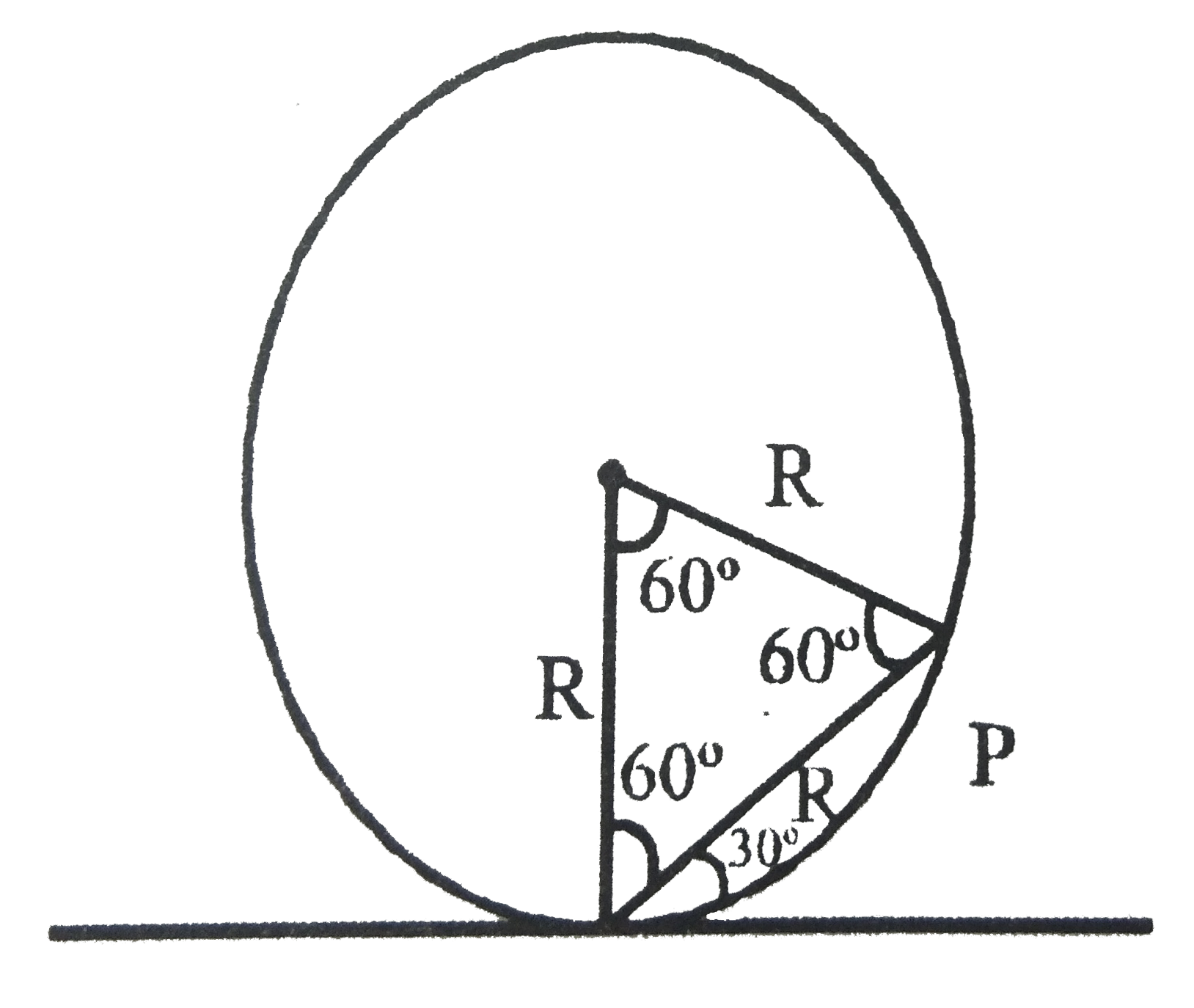 ltbgt (D)
ltbgt (D)