Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A solid sphere of radius 3R, a solid disc of radius 2R and a ring of r...
Text Solution
|
- The ratio of the accelerations for a solid sphere (mass m, and radius ...
Text Solution
|
- A solid sphere of radius 3R, a solid disc of radius 2R and a ring of r...
Text Solution
|
- A solid sphere of radius 3R , a solid disc of radius 2R and a ring of ...
Text Solution
|
- The ratio of the time taken by a solid sphere and that taken by a disc...
Text Solution
|
- The ratio of the acceleration for a solid sphere (mass m and radius R)...
Text Solution
|
- If a ring, a disc, a solid sphere and a cyclinder of same radius roll ...
Text Solution
|
- The ratio of the acceleration for a solid sphere (mass m and radius R ...
Text Solution
|
- The ratio of the acceleration for a solid sphere (mass m and radius R)...
Text Solution
|
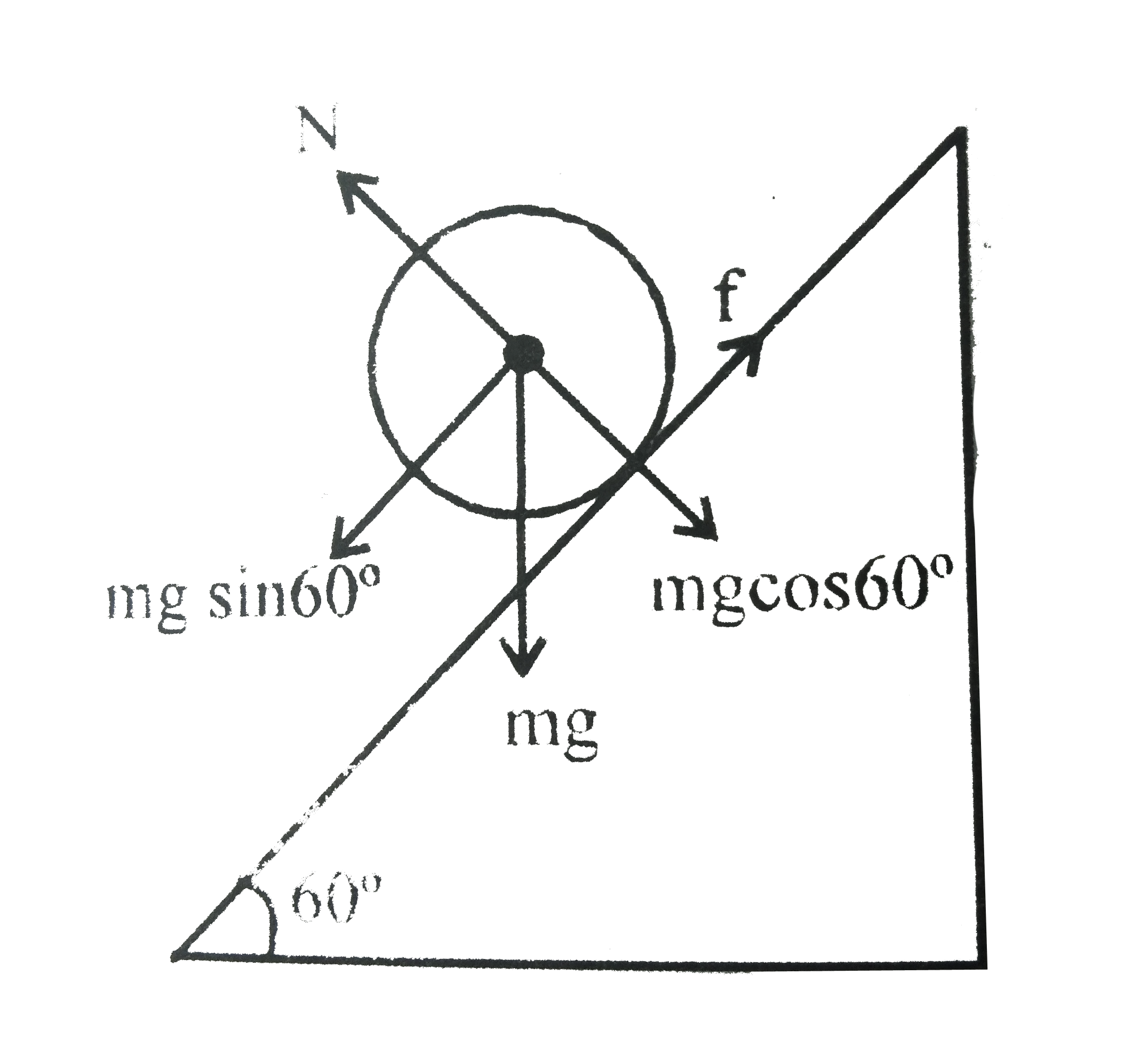 .
.