Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
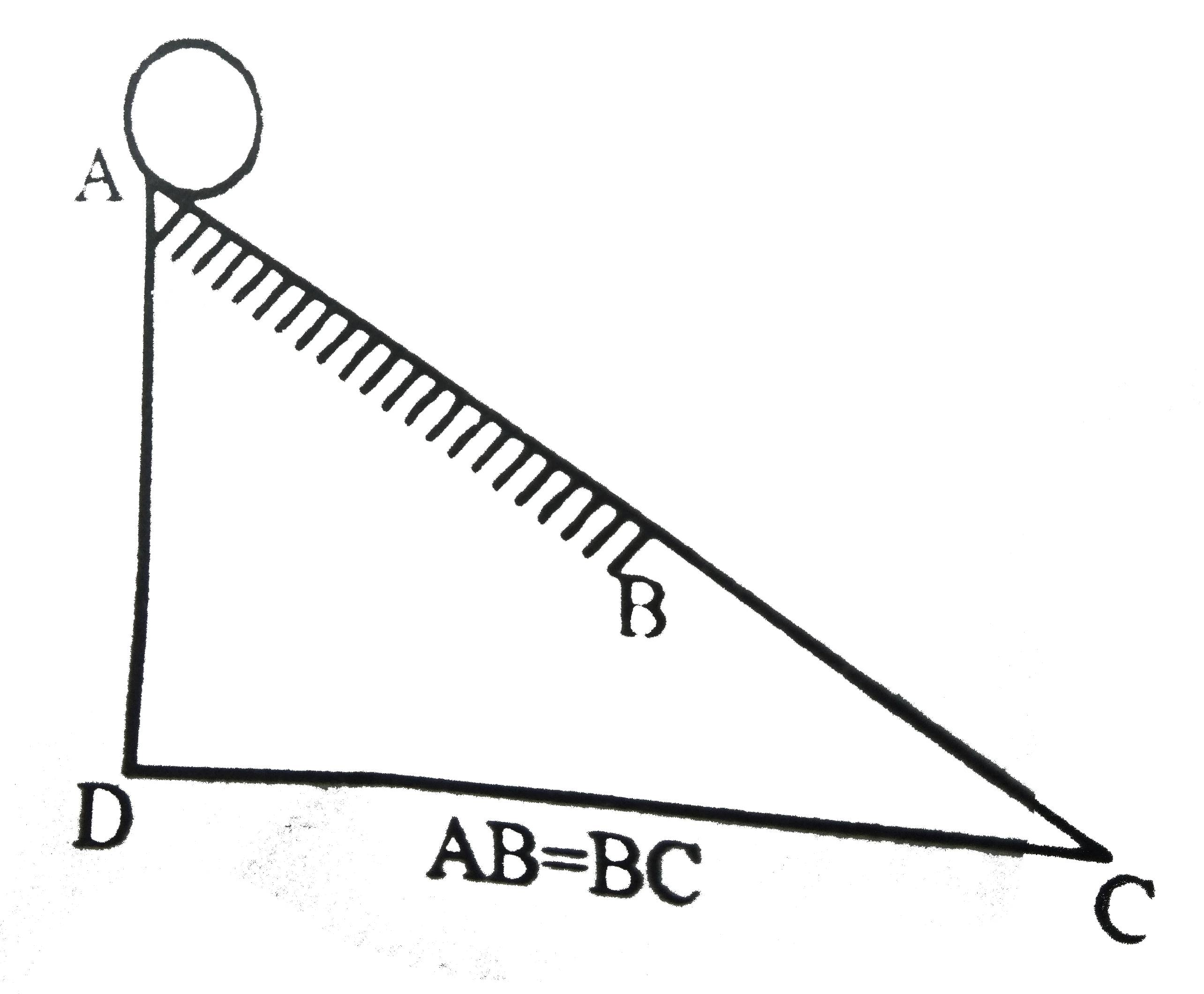
- Portion AB of the wedge shown in figure is rough and BC is smooth. A s...
Text Solution
|
- When a sphere rolls without slipping the ratio of its kinetic energy o...
Text Solution
|
- The moment of inertia of a solid cylinder about its axis is given by (...
Text Solution
|
- Portion AB of the wedge shown in figure is rough and BC is smooth. A s...
Text Solution
|
- Portion AB of the wedge shown in figure is rough and Bc is smooth. A s...
Text Solution
|
- A solid sphere is rolling without slipping on a horizontal plane. The ...
Text Solution
|
- When a solid cylinder rolls without slipping the ratio of kinetic ener...
Text Solution
|
- A hollow sphere is rolling without slipping on a rough surface. The ra...
Text Solution
|
- In both the figure all other factors are same, except that in figure (...
Text Solution
|
 .
.