Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
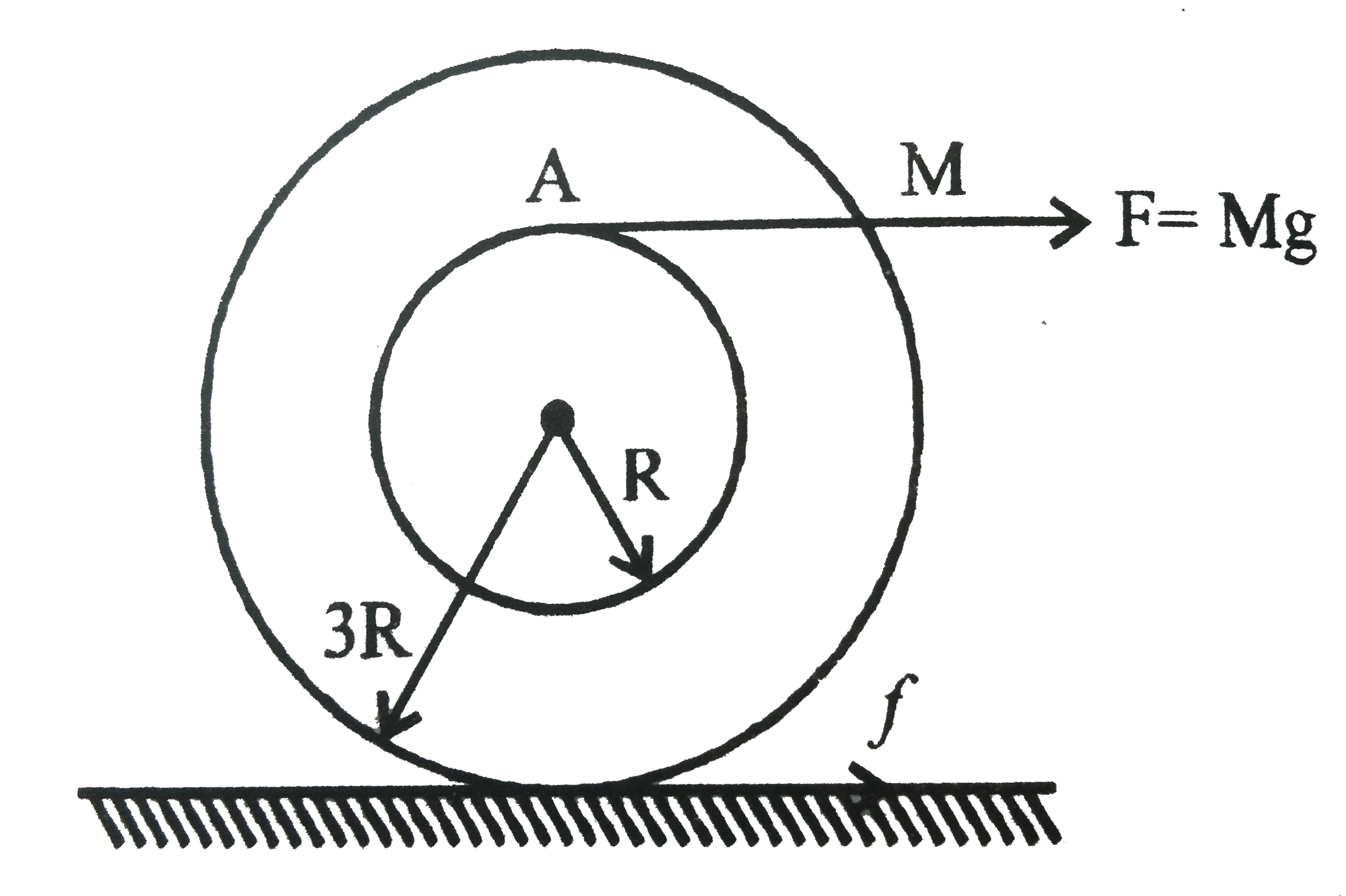
- A spool of inner radius R and outer radius 3R has a moment of inertia ...
Text Solution
|
- The figure shows a spool placed at rest on a horizontal rough surface....
Text Solution
|
- Inner and outer radii of a spool are r and R I, respectively. A thread...
Text Solution
|
- Inner and outer radii of a spool are r and R respectively. A thread is...
Text Solution
|
- A spool of inner radius R and outer radius 3R has a moment of inertia ...
Text Solution
|
- A spool with thread wound on it, of mass m, rests on a rough horizonta...
Text Solution
|
- Consider an arrangement shown in the figure. The pulley P is frictionl...
Text Solution
|
- A spool is kept in equilibrium on an incline plane as shown in figure....
Text Solution
|
- A spool of mass m has moment of inertia I= 2mR^(2) about its axis of s...
Text Solution
|
 .
.