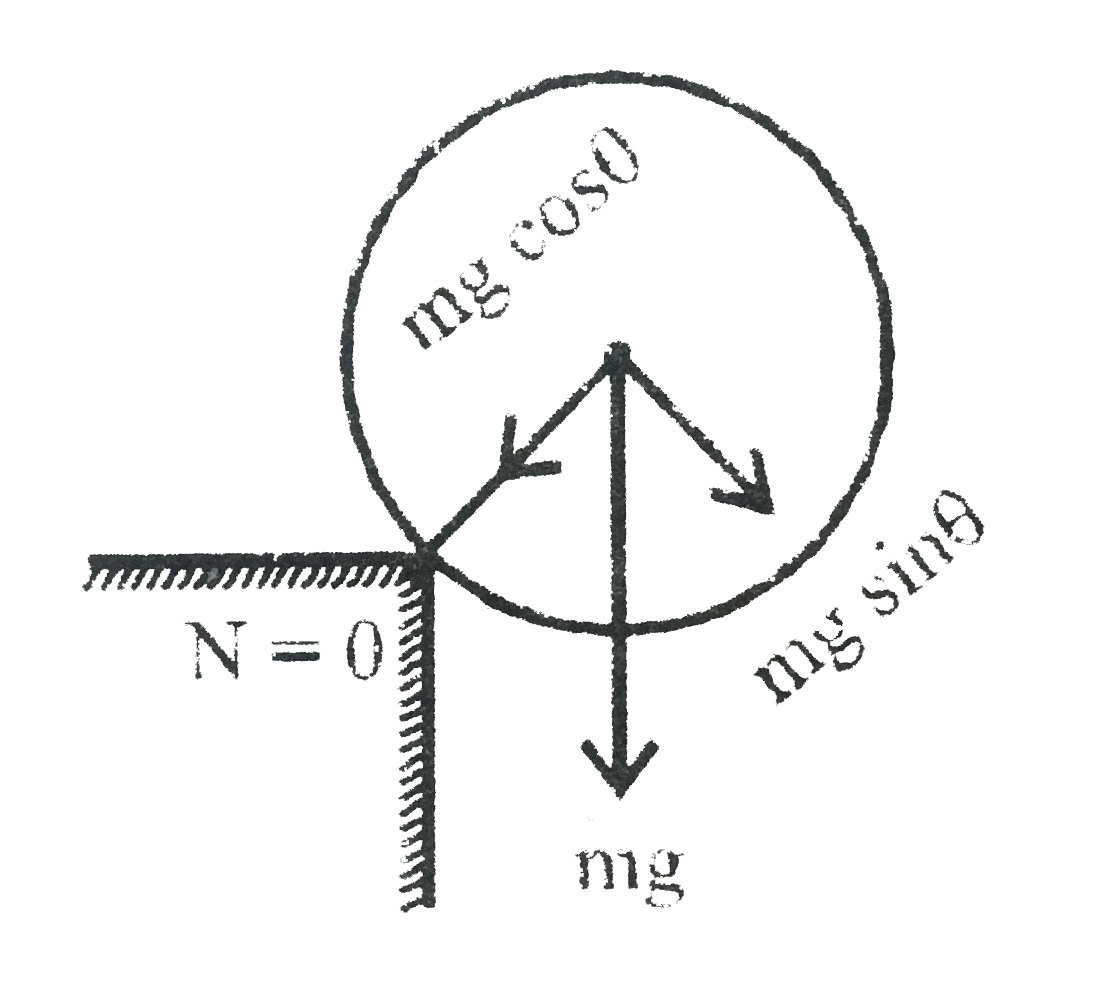
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- A rectangular rigid fixed block has a long horizontal edge. A solid ho...
Text Solution
|
- A rectangular rigid fixed block has a long horizontal edge. A solid ho...
Text Solution
|
- A cylinder of mass M and radius R is resting on two corner edges A and...
Text Solution
|
- A rectangular rigid fixed block has a long horizontal edge. A solid ho...
Text Solution
|
- A horizontal plane supports a stationary vertical cylinder of radius R...
Text Solution
|
- M.I. of a uniform horizontal solid cylinder of mass M about an axis pa...
Text Solution
|
- A horizontal uniform rod of mass 'm' has its left end hinged to the fi...
Text Solution
|
- A cylinder with radius R spins about its horizontal axis with angular ...
Text Solution
|
- Moment of inertial of a uniform horizontal solid cylinder of mass M ab...
Text Solution
|