Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
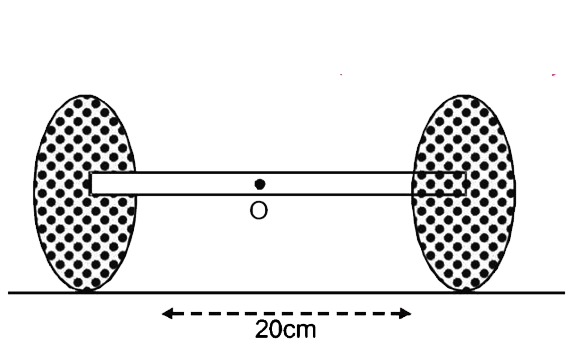
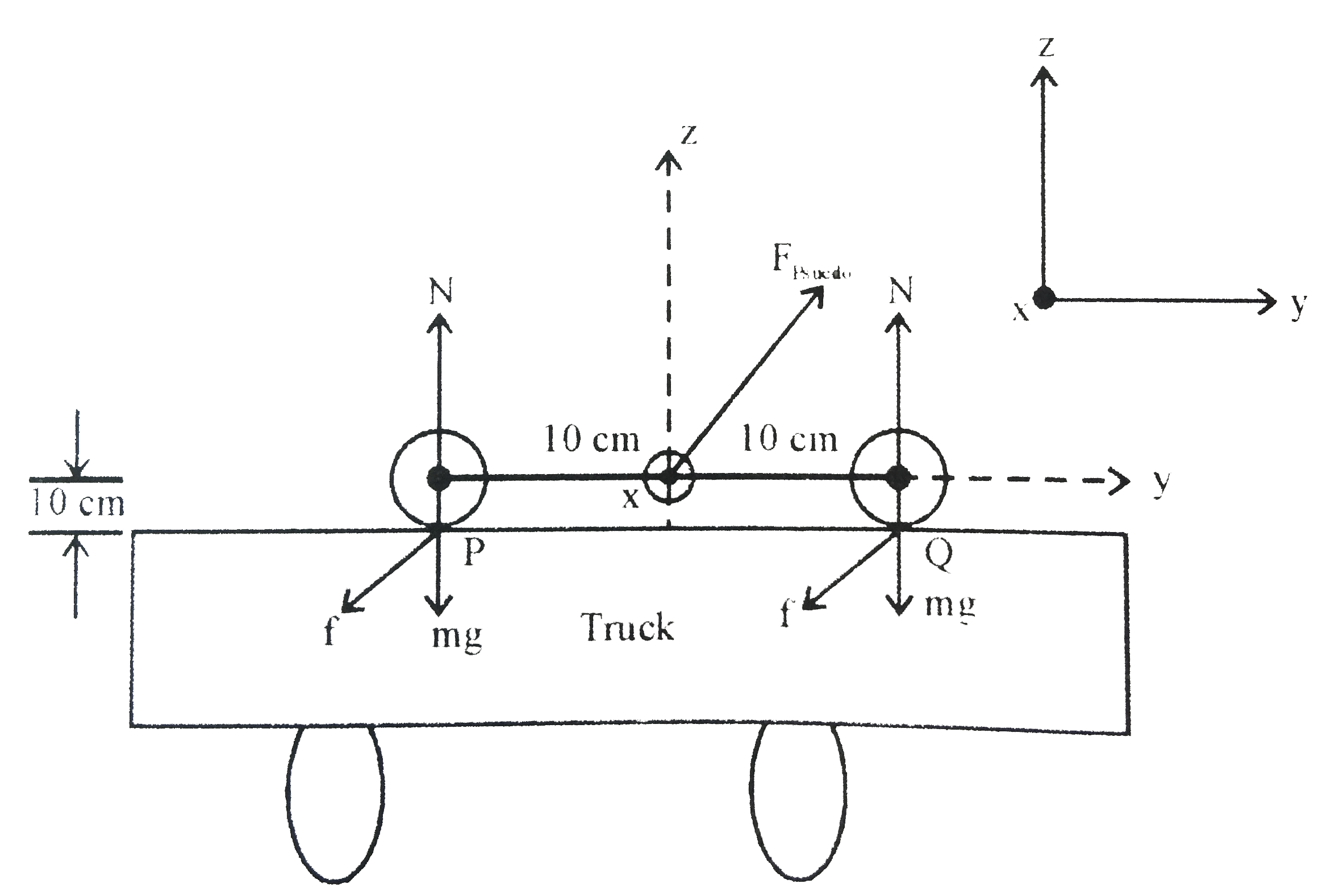
- Two thin circular disks of mass 2kg and radius 10 cm each are joined b...
Text Solution
|
- Two thin circular disks of mass 2kg and radius 10 cm each are joined b...
Text Solution
|
- Find the moment of inertia of a circular disk or solid cylinder of rad...
Text Solution
|
- Two thin circular disks of mass 2kg and radius 10 cm each are joined b...
Text Solution
|
- The moment of inertia of a thin uniform rod of mass M and length L abo...
Text Solution
|
- Calculate the moment of inertia of a thin rod of mass m and length l a...
Text Solution
|
- किसी छड़ की लम्बाई मे लम्बवत, द्रव्यमान केंद्र से गुजरने वाली अक्ष के प...
Text Solution
|
- 100 ग्राम द्रव्यमान तथा 100 सेमी लम्बाई की पतली छड़ का इसकी लम्बाई के ...
Text Solution
|
- द्रव्यमान M तथा त्रिज्या R की एक वृत्तीय चकती का चकती के किनारे से गुज...
Text Solution
|