Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
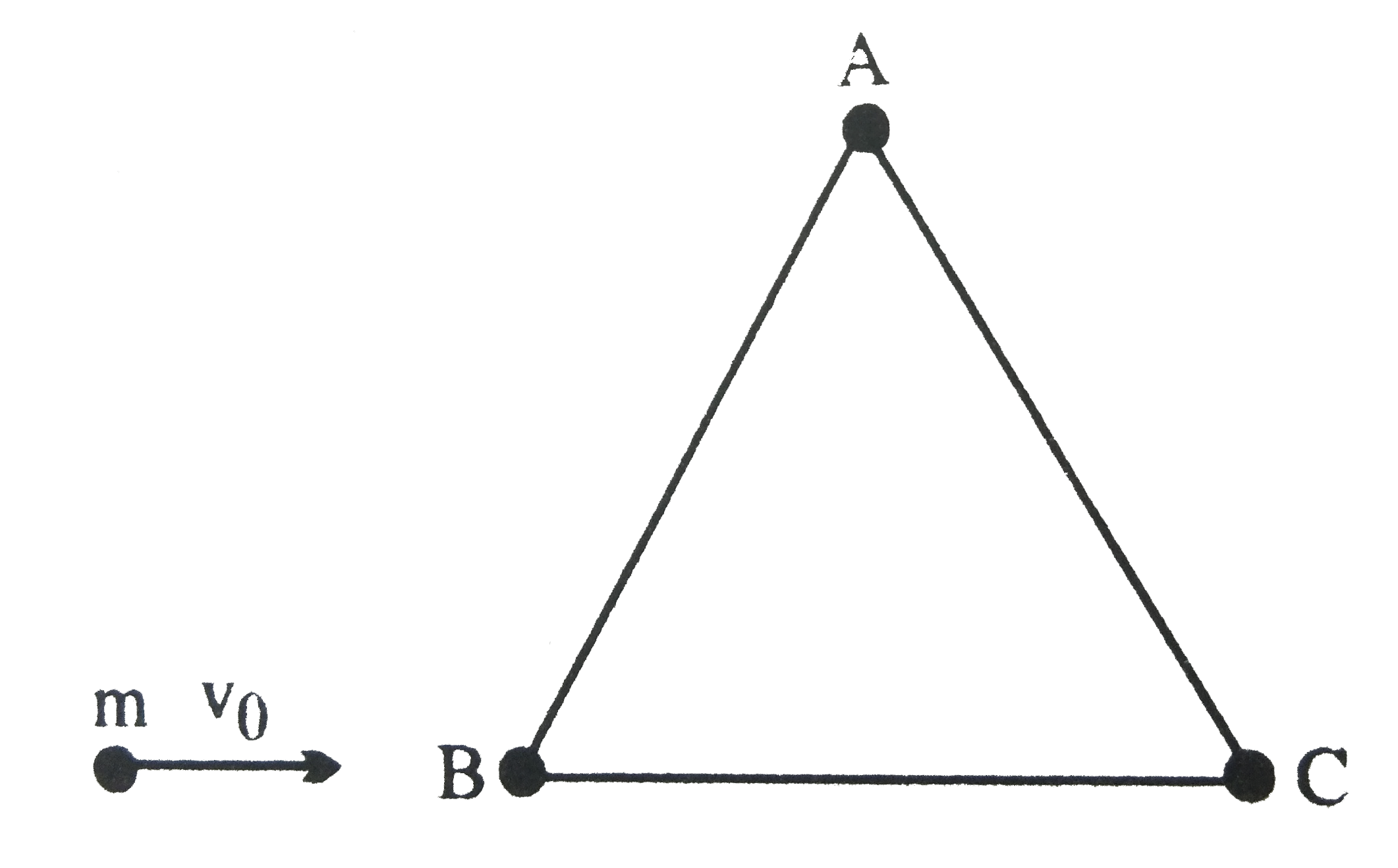
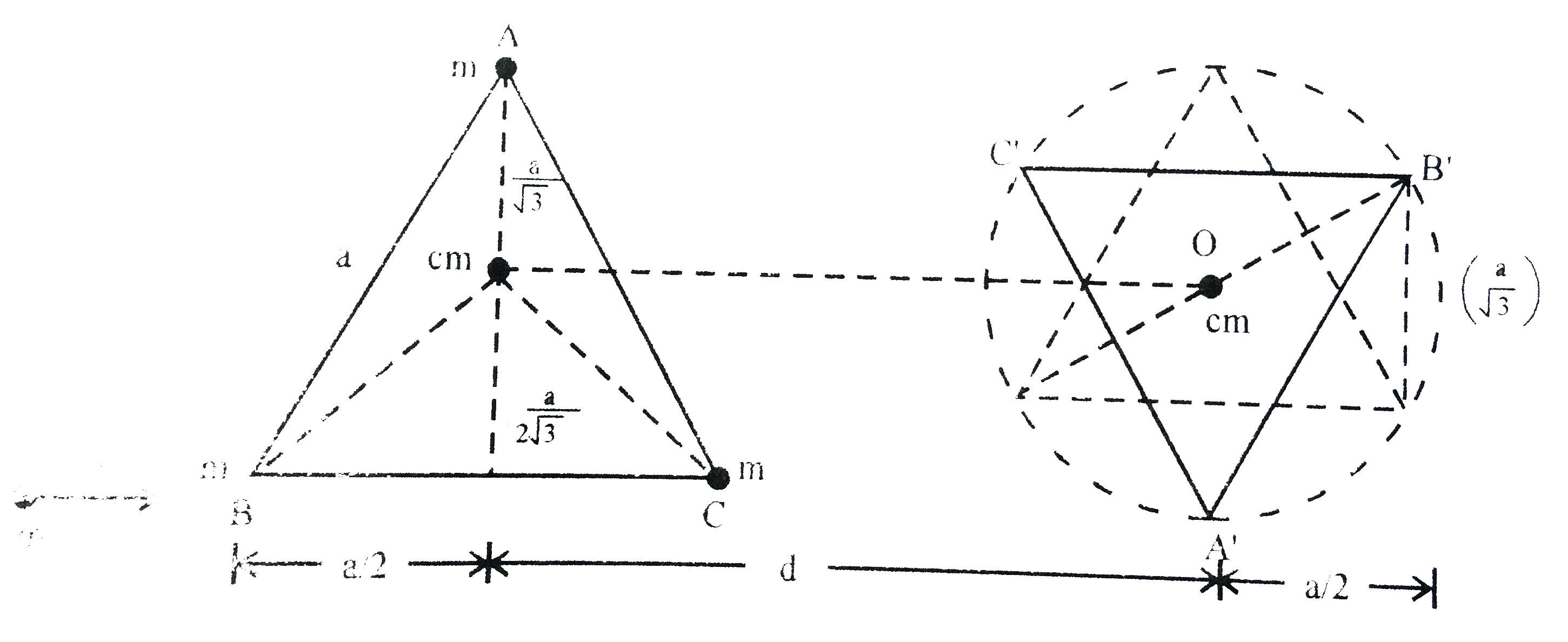
- Three particles A,B,C of mass m each are joined to each other by massl...
Text Solution
|
- Three particles A, B and C are situated at the vertices of an equilate...
Text Solution
|
- Three particles A,B,C of mass m each are joined to each other by massl...
Text Solution
|
- If there particles, each of mass M, are placed at the three corners of...
Text Solution
|
- Three particles each of mass m are palced at the corners of an equilat...
Text Solution
|
- Three identical particles each of mass m are placed at the vertices of...
Text Solution
|
- Three particles each of mass m are kept at vertices of an equilateral ...
Text Solution
|
- समान द्रव्यमान m के दो कण A तथा B जो एक सरल रेखा में एक-दूसरे की और क्...
Text Solution
|
- Three particles each of mass m are placed at the three corners of an e...
Text Solution
|