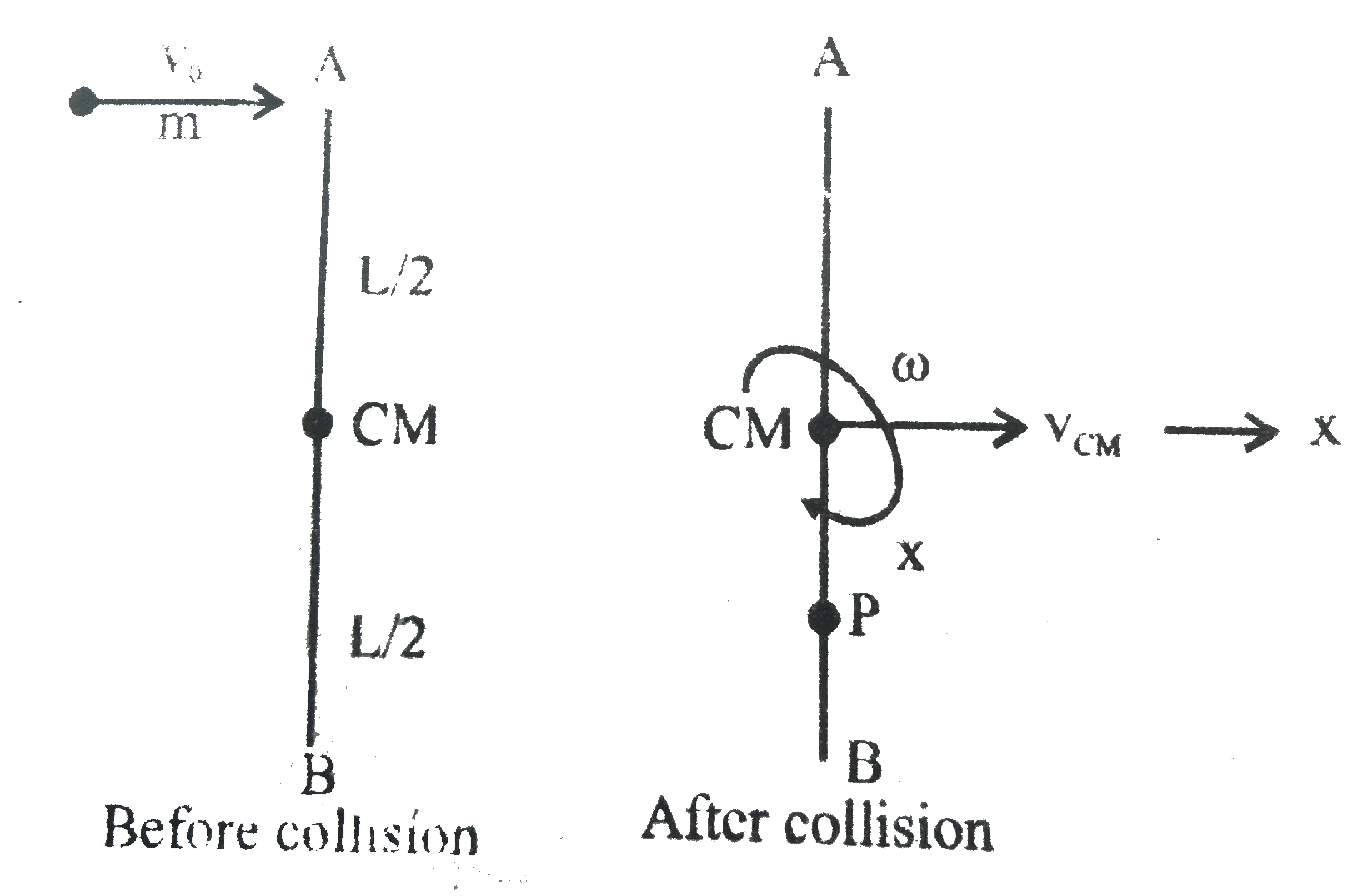
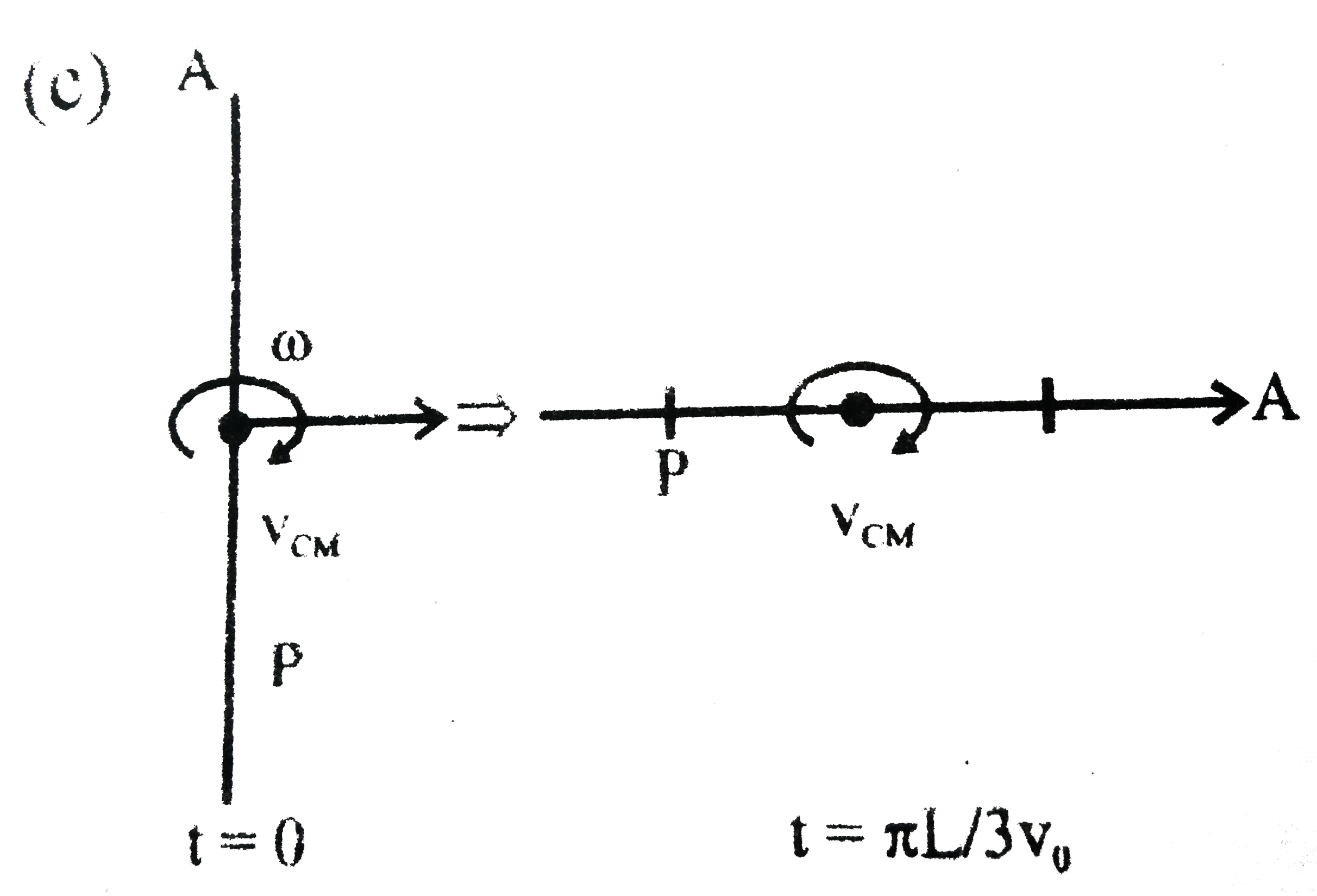
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A rod AB of mass M and length L is lying on a horizontal frictionless ...
Text Solution
|
- A rod AB of mass M and length L is lying on a horizontal frictionless ...
Text Solution
|
- A uniform rod AB of length L and mass M is lying on a smooth table. A ...
Text Solution
|
- A rod AB of mass M and length L is lying on a horizontal frictionless ...
Text Solution
|
- A uniform rod of mass M is hinged at its upper end. A particle of mass...
Text Solution
|
- A rod AB of length 2L and mass m is lying on a horizontal frictionless...
Text Solution
|
- द्रव्यमान M तथा लम्बाई L की एक छड़ AB एक घर्षणहीन तल पर पड़ है। द्रव्यमा...
Text Solution
|
- A uniform rod of mass m and length L is at rest on a smooth horizontal...
Text Solution
|
- M द्रव्यमान व L लम्बाई की एक छड़ AB क्षैतिज घर्षणहीन सतह पर रखी हुई है...
Text Solution
|