Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
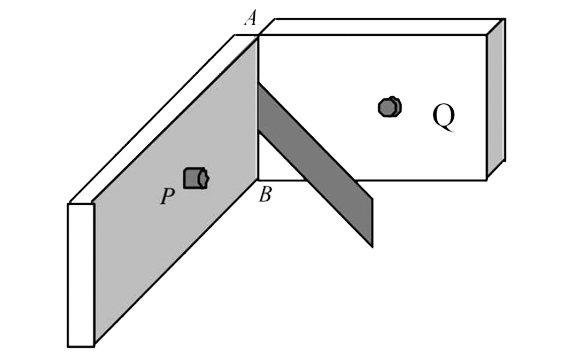
- Two heavy metallic plates are joined together at 90^@ to each other. A...
Text Solution
|
- Two heavy metallic plates are joined together at 90^@ to each other. A...
Text Solution
|
- Two partcles of masses 1 kg and 2 kg are placed at a distance of 3 m. ...
Text Solution
|
- Let I be the moment of interia of a uniform square plate about an axis...
Text Solution
|
- The moment of inertia of a dumb bell consisting of two identical unifo...
Text Solution
|
- एक समान वर्गाकार प्लेट का एक अक्ष AB के परितः जो इसक केंद्र से गुजरती ...
Text Solution
|
- धातु की दो भारी प्लेटें परस्पर 90^(@) पर जुड़ी है। 30 किग्रा द्रव्यमान ...
Text Solution
|
- एक समरूप वर्गाकार प्लेट का AB अक्ष के परितः जड़त्व आघूर्ण I है। AB वह ...
Text Solution
|
- Moment of inertia of a thin uniform rectangular sheet about an axis pa...
Text Solution
|