Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A wodden log mass M and length L is hinged by a frictionless nail at O...
Text Solution
|
- A wooden log of mass M and length L is hinged by a frictionless nail a...
Text Solution
|
- A circular wooden hoop of mass m and radius R rests fiat on a friction...
Text Solution
|
- A uniform rod of length L lies on a smooth horizontal table. The rod h...
Text Solution
|
- A particle of mass m moving with velocity v strikes a stationary parti...
Text Solution
|
- A wodden log mass M and length L is hinged by a frictionless nail at O...
Text Solution
|
- A wooden log of mass M and length L is hinged by a frictionless nail a...
Text Solution
|
- A circular hoop of mass m and radius R rests flat on a horizontal fric...
Text Solution
|
- A rod of mass m and length l hinged at the centre is placed on a horiz...
Text Solution
|
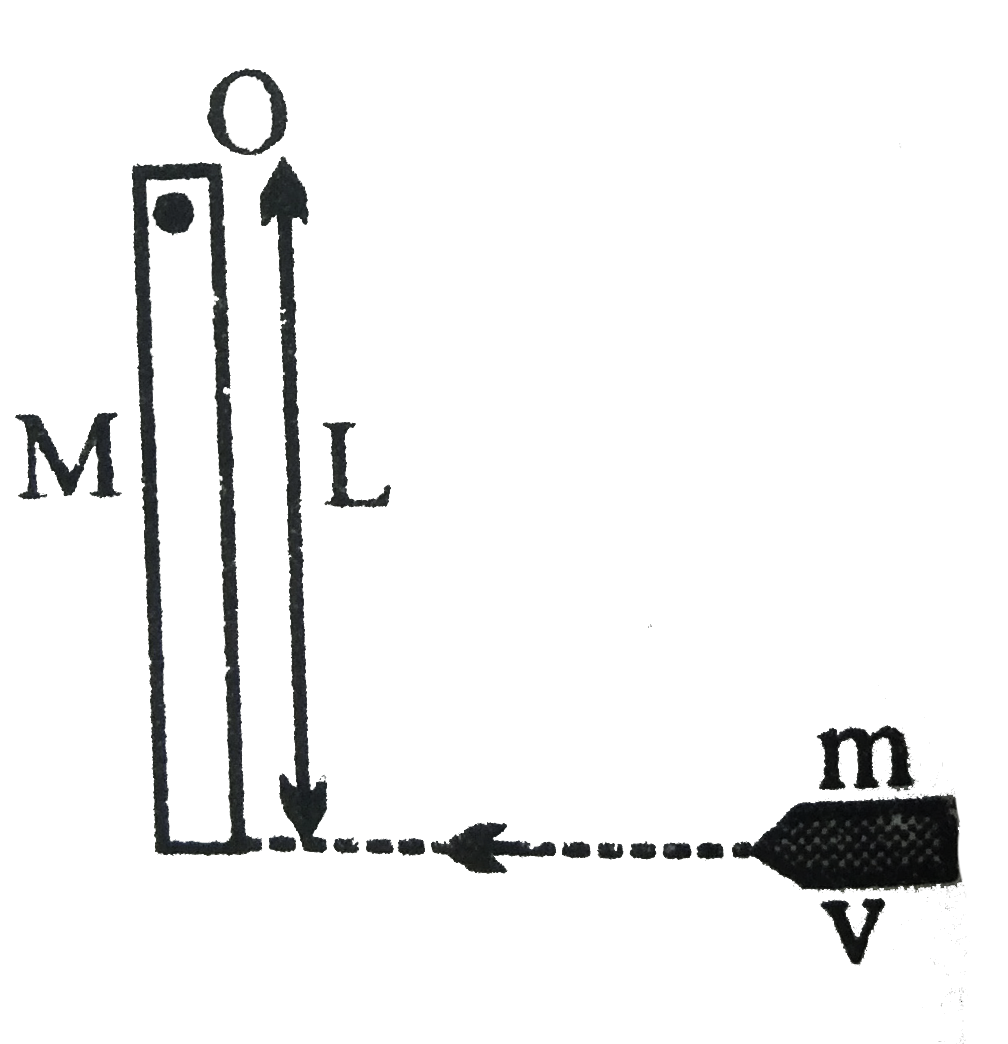 .
.