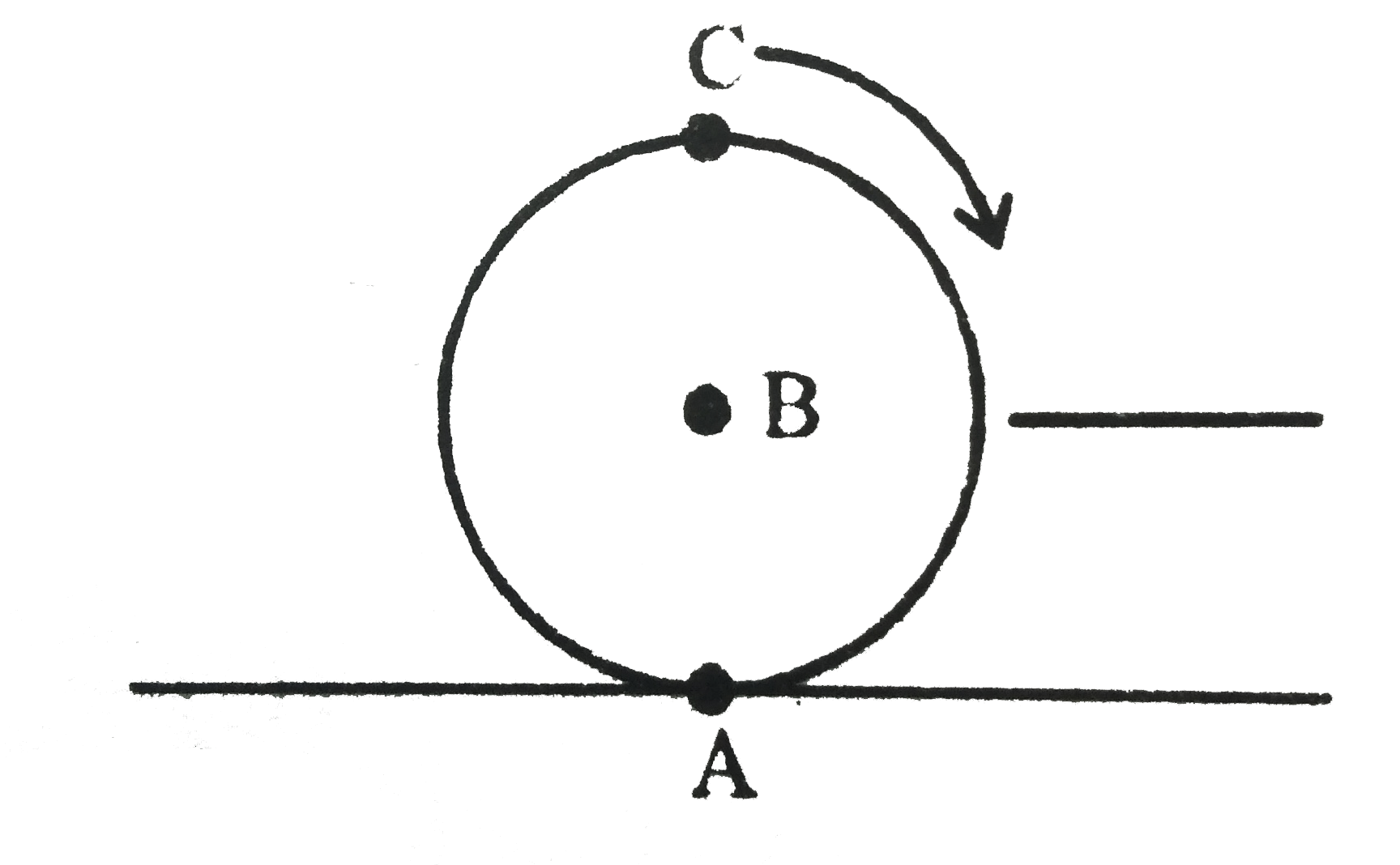
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
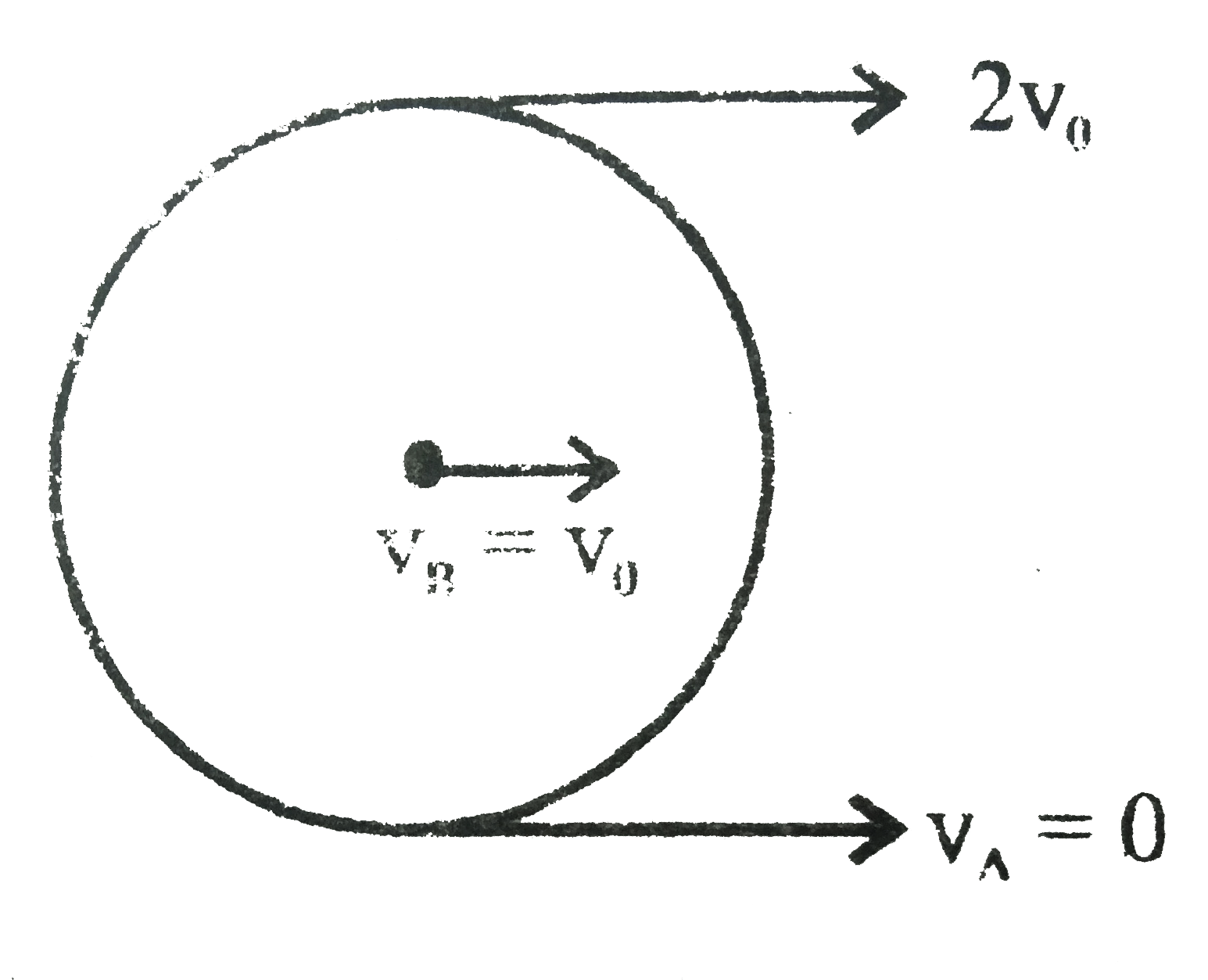
- A sphere is rolling without slipping on a fixed horizontal plane surfa...
Text Solution
|
- A sphere is rolling without slipping on a fixed horizontal plane surfa...
Text Solution
|
- A force F acts tangentially at the highest point of a sphere f mass m ...
Text Solution
|
- A sphere of mass M rolls without slipping on rough surface with centre...
Text Solution
|
- A solid sphere rolling on a rough horizontal surface. Acceleration of ...
Text Solution
|
- A sphere is rolling without slipping on a fixed horizontal plane surfa...
Text Solution
|
- A sphere is rolling without slipping on a fixed horizontal plane surfa...
Text Solution
|
- m द्रव्यमान और त्रिज्या का एक गोला क्षैतिज तल पर ॥ वेग से बिना फिसले ल...
Text Solution
|
- एक स्थिर क्षैतिज समतल पृष्ठ पर एक गोला बिना फिसले लुढ़क रहा है। चित्र ...
Text Solution
|
 .
. .
.