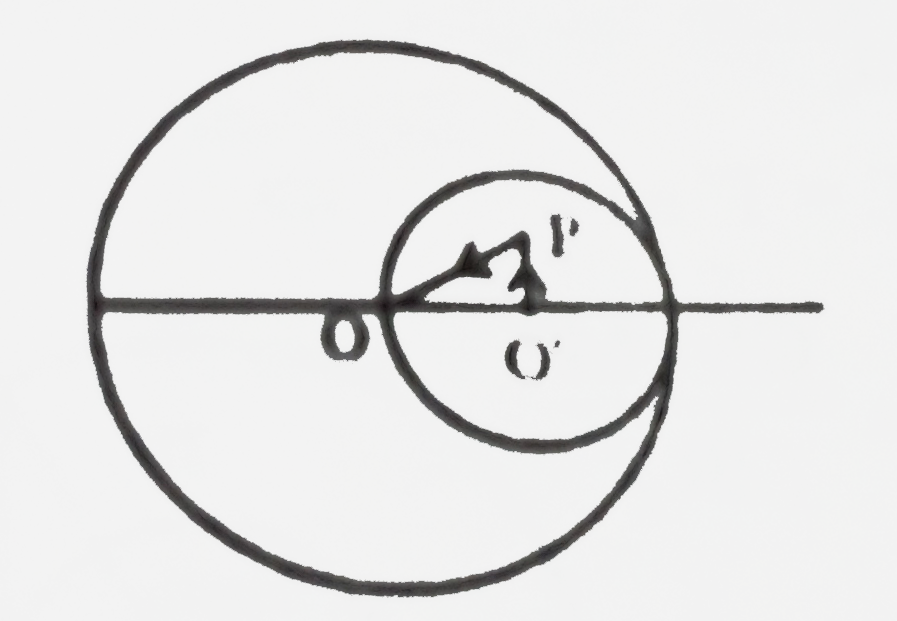Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A sphere of radius R has its centre at the origin. It has a uniform ma...
Text Solution
|
- The figure represents a solid uniform sphere of mass M and radius R. A...
Text Solution
|
- A uniform metal sphere of radius R and mass m is surrounded by a thin ...
Text Solution
|
- A sphere of radius R has its centre at the origin. It has a uniform ma...
Text Solution
|
- A uniform sphere has a mass M and radius R. Find the pressure p inside...
Text Solution
|
- Inside a uniform sphere of density rho there is a spherical cavity who...
Text Solution
|
- A spherical hole is made in a solid sphere of radius R. The mass of th...
Text Solution
|
- Mass density of sphere having radius R varies as rho = rho0(1-r^2/R^2)...
Text Solution
|
- A uniform disc of radius R has a hole cut out which has a radius r. Th...
Text Solution
|